TrainMRF UGM Demo

Up to this point, we have focused on the tasks of decoding/inference/sampling, given known potential functions. That is, we have assumed that the model is known, and/or made up a story to justify our choice of potential functions. We now turn to the task of parameter estimation. In parameter estimation, we are given data (and a graph structure), and we want to find the 'best' potential functions for modeling the data. For example, we might want to find the potential functions that maximize the likelihood of the data. Once we have estimated a good set of potential functions, we can then use these potentials with the techniques discussed in the previous demos for decoding/inference/sampling.

Typically, using data to estimate good potential functions will lead to a much better model than if we tuned the potential functions manually. This is true for several reasons, but one of the main reasons is simply that in most models it is difficult to describe what the values of the potential functions mean in probabilistic terms (of course, there are some exceptions like Markov chains). However, parameter estimation will generally be harder than decoding/inference/sampling with known parameters. Indeed, most parameter estimation methods will need to use decoding/inference/sampling as a sub-routine. Further, we also must address the modeling issue of tieing/parameterizing the potential functions.

Vancouver Rain Data

Our first example of parameter estimation we will consider a simple model of rainfall in Vancouver. I extraced the "daily precipitation" amount for the Steveston weather station (which is close to the Vancouver airport) from the Canadian daily climate archive (CDCA) from Canada's National Climate Archive. This archive contained data for this weather station from 1896-2004, and I made a simple binary data set out of the available data as follows: I treated each month as a sample, and concentrated on the first 28 days of the month so that all samples would be the same length. I also removed the months with missing or accumulated values, and binarized the data set by giving it the state '0' if there was no daily precipitation (or trace amounts), and '1' if there was non-zero daily precipitation. After removing the missing months, we are left with a data set containing 1059 months (samples) with 28 days (variables).

We can load this data set into a variable y using:

load rain.mat
y = int32(X+1); % Convert from {0,1} double to {1,2} int32 representation

In UGM the data should is stored in the int32 format, and should be in the range {1,2,...,nStates}.

Below is a plot of the first 100 months:

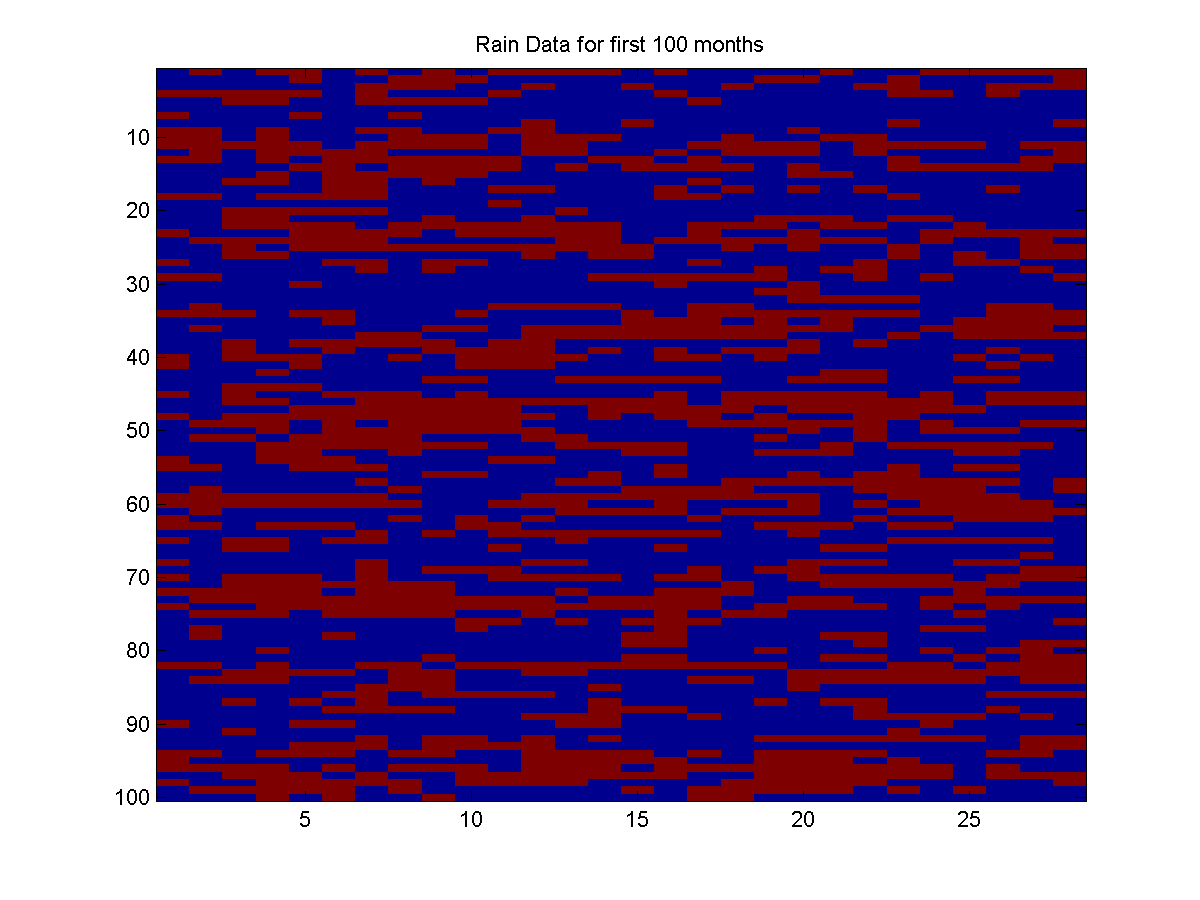
In this plot, `rain' (state 2) is represented by the color red, while `no rain' (state 1) is represented by the color blue. One of the simplest models we could fit to this data set would simply treat each day as an independent sample from a Bernoulli distribution. Here, we simply calculate the probability that it will rain as the average across all the days:

p_rain = sum(y(:)==2)/numel(X)

p_rain =

    0.4115

So, we have a non-zero daily precipitation on ~41% of the days. We can calculate the log-likelihood of the full data set under this simple model as follows: negloglik_y = -log(p_rain)*sum(y(:)==2) - log(1-p_rain)*sum(y(:)==1) negloglik_y = 2.0086e+004
Below is 100 samples drawn from this simple independent distribution:

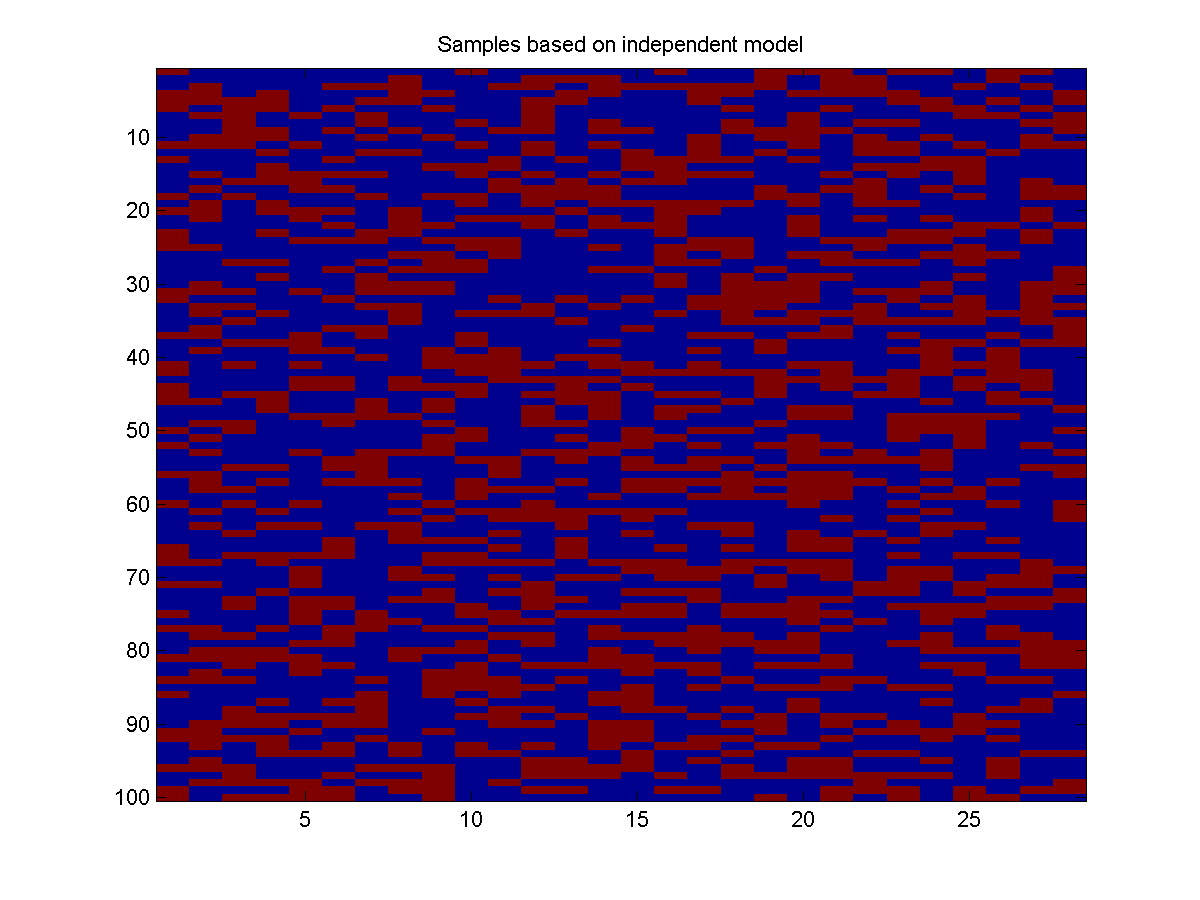
These samples look less 'clumpy' than the real data. This makes sense, the independent model does not take into account that if it rained yesterday, it is more likely to rain today. To take into account this dependency, we will use a UGM to model the statistical dependency between adjacent days. However, unlike previous demos where we chose a set of node/edge potentials that we hoped would be a good model of real data, in this demo we will use the real data to find the node/edge potentials that maximize the likelihood of the data. That is, we will give UGM the data, tell it to use a chain-structured dependency (as well as some extra information about how to construct the potentials), and the output will be a set of parameters. We can then use these parameters to form our potentials and use our usual (conditional) decoding/inference/sampling with the potentials.

As always, our first step will be to build the edgeStruct that keeps track of information about the graphical structure. We will assume a chain-structured dependency:

[nInstances,nNodes] = size(y);
nStates = max(y);
adj = zeros(nNodes);
for i = 1:nNodes-1
    adj(i,i+1) = 1;
end
adj = adj+adj';
edgeStruct = UGM_makeEdgeStruct(adj,nStates);

Making the nodeMap and edgeMap

To do parameter estimation with UGM, we need to define the nodeMap and edgeMap arrays. These int32 arrays are the same size as the corresponding nodePot and edgePot, and each corresponding element of the maps tells us which element of the parameter vector w that we exponentiate to make the potentials. In particular, UGM uses the following rule to make the potentials from the parameters:

We set nodePot(n,s) = exp(w(nodeMap(n,s))).
We set edgePot(s1,s2,e)= exp(w(edgeMap(s1,s2,e)).

Since we allow nodeMap(n,s)=0, it is assumed above that w(0)=0. Note that this parameterization will allow us to state maximum likelihood estimation as a convex optimization problem.

In our example, we will define the nodeMap as follows:

maxState = max(nStates);
nodeMap = zeros(nNodes,maxState,'int32');
nodeMap(:,1) = 1;

By setting the first column of the nodeMap to the value 1, we are indicating that the potential of being in the `no rain' state will be given by exponentiating the first element of the parameter vector w. Note that this means that all days of the month share the same potential for this state. Setting an element of the nodeMap to 0 means that the corresponding potential is fixed at 0. When doing maximum likelihood estimation, the global normalization allows to arbitrarily fix one of the states for each node without affecting the final result. Note that when doing parameter estimation, we can allow the nStates variable to be a vector, in case some variables have fewer than others.

In our example, we will first define the edgeMap as follows:

nEdges = edgeStruct.nEdges;
edgeMap = zeros(maxState,maxState,nEdges,'int32');
edgeMap(1,1,:) = 2;
edgeMap(2,2,:) = 2;

That is, we will make all edges use the second element of the parameter vector w for the potential of adjacent days being in the same state. And further, we will fix the potential of adjacent days having different states.

Initializing Weights

After defining the nodeMap and edgeMap variables which map parameters to potentials, we next initialize the parameter vector (typically to a vector of zeroes). The parameter vector must have the right size, and we can initialize it as follows: nParams = max([nodeMap(:);edgeMap(:)]); w = zeros(nParams,1);
Since our maps required two variables, in our example w will simply be a two-element vector.

We can use the maps and the parameter vector to make the potentials as follows:

[nodePot,edgePot] = UGM_MRF_makePotentials(w,nodeMap,edgeMap,edgeStruct);

Since we initialized w to zero, this just makes a nodePot and edgePot that contain all ones.

Computing Sufficient Statistics

When training unconditional UGMs, which we will refer to as Markov random fields, the parameter estimation only depends on the data through a set of sufficient statistics. We can use the data to compute the sufficient statistics using: suffStat = UGM_MRF_computeSuffStat(y,nodeMap,edgeMap,edgeStruct);
Once we have the sufficient statistics, we can compute the negative log-likelihood of the data using: nll = UGM_MRF_NLL(w,nInstances,suffStat,nodeMap,edgeMap,edgeStruct,@UGM_Infer_Chain) nll = 2.0553e+04
This is higher than the independent model we had before, meaning that the naive model with all potentials equal does a poorer job of predicting the data than the independent model. Note that the last argument of the UGM_MRF_NLL function is an anonymous function that will be used for inference in the model (in this case, the model is a chain so we used UGM_Infer_Chain).

Maximum Likelihood Estimation

To find the maximum likelihood estimator, we minimize the negative log-likelihood function. We can do this using the minFunc package: w = minFunc(@UGM_MRF_NLL,w,[],nInstances,suffStat,nodeMap,edgeMap,edgeStruct,@UGM_Infer_Chain) Iteration FunEvals Step Length Function Val Opt Cond 1 2 1.16857e-04 1.79845e+04 1.63026e+03 2 3 1.00000e+00 1.78218e+04 3.67640e+02 3 4 1.00000e+00 1.78108e+04 2.88642e+01 4 5 1.00000e+00 1.78108e+04 4.99058e+00 5 6 1.00000e+00 1.78108e+04 4.94596e-02 6 7 1.00000e+00 1.78108e+04 1.37016e-03 Directional Derivative below progTol w = 0.1590 0.8504
The first argument of the minFunc function is the function to minimize, the second argument is the initial parameter vector, the third argument is a structure containing non-default parameters of the optimization routine (i.e. you can turn off the program output), and the remaining arguments are passed as arguments to the function that is being minimized.

Looking at the Function Val column in the output of minFunc, we see that the negative log-likelihood with the estimated parameters is much lower than the initial parameters, and also much lower than with the independent model.

If we want to, we can make and look at the potentials based on the estimated parameters:

[nodePot,edgePot] = UGM_MRF_makePotentials(w,nodeMap,edgeMap,edgeStruct);
nodePot(1,:)
edgePot(:,:,1)

ans =

    1.1723    1.0000


ans =

    2.3406    1.0000
    1.0000    2.3406

Looking at the potentials, we see that the node potential is higher for the state 'no rain', and the edge potentials are higher for adjacent days having the same value. Although this is exactly what we expect, by optimizing the parameters we in some sense have found the 'best' parameters.

Training with more expressive edge potentials

The Ising-like edge potentials in the previous section assumes the states are interchangeable. That is, the potential of seeing (rain,rain) is the same as (no rain, no rain), and further the potential of seeing (rain,no rain) is the same as seeing (no rain, rain). We can relax this assumption by using additional parameters. Below, we change the edgeMap array so that we use a different parameter for each combination of states in the edge potential (though we still tie the potentials across edges). Note that we only need to parameterize 3 out of the 4 combinations of states, because of the global normalization. In particular, we will fix the potential (rain,rain) state. % Use different parameters for different combinations of states edgeMap(2,2,:) = 0; edgeMap(1,2,:) = 3; edgeMap(2,1,:) = 4; % Initialize weights nParams = max([nodeMap(:);edgeMap(:)]); w = zeros(nParams,1); % Compute sufficient statistics suffStat = UGM_MRF_computeSuffStat(y,nodeMap,edgeMap,edgeStruct); % Optimize w = minFunc(@UGM_MRF_NLL,w,[],nInstances,suffStat,nodeMap,edgeMap,edgeStruct,@UGM_Infer_Chain) Iteration FunEvals Step Length Function Val Opt Cond 1 2 7.12949e-05 1.89590e+04 3.14727e+03 2 3 1.00000e+00 1.85381e+04 1.26201e+03 3 4 1.00000e+00 1.81469e+04 1.28848e+03 4 5 1.00000e+00 1.79040e+04 1.23205e+03 5 6 1.00000e+00 1.78407e+04 2.22810e+02 6 7 1.00000e+00 1.78393e+04 4.11467e+01 7 9 1.00000e+01 1.78379e+04 1.01343e+02 8 10 1.00000e+00 1.78333e+04 1.61229e+02 9 11 1.00000e+00 1.78192e+04 2.38441e+02 10 12 1.00000e+00 1.78089e+04 1.72145e+02 11 13 1.00000e+00 1.78018e+04 5.25205e+01 12 14 1.00000e+00 1.77996e+04 3.54473e+01 13 15 1.00000e+00 1.77988e+04 5.37657e+01 14 16 1.00000e+00 1.77980e+04 4.41137e+01 15 17 1.00000e+00 1.77977e+04 7.91935e+00 16 18 1.00000e+00 1.77977e+04 4.92522e-01 17 19 1.00000e+00 1.77977e+04 2.56970e-02 18 20 1.00000e+00 1.77977e+04 4.31682e-03 19 21 1.00000e+00 1.77977e+04 1.71722e-04 Directional Derivative below progTol w = 0.5968 -0.4499 -1.0029 -1.1506
Since this model contains the previous model as a special case, we expect (and observe) an improvement in the training set negative log-likelihood (ie. Function Val). As before we can look at the potentials as follows: [nodePot,edgePot] = UGM_MRF_makePotentials(w,nodeMap,edgeMap,edgeStruct); nodePot(1,:) edgePot(:,:,1) ans = 1.8163 1.0000 ans = 0.6377 0.3668 0.3165 1.0000
We see that (rain,rain) configuration receives a higher potential than the (no rain, no rain) configuration. It might have been difficult to guess at this asymmetry if we had chosen the potentials heuristically without looking at actual data. In contrast, the potential of (no rain,rain) is fairly close to the potential of (rain,no rain).

Using untied parameters to model boundary effects

Our model assumes that the node potentials are the same for all days of the month. However, we may want to allow the node potentials for the first and last day of the month to be different, since they only have one neighbor in the graph. We can do this by just adding an extra parameter: nodeMap(1,1) = 5; nodeMap(end,1) = 5; % Initialize weights nParams = max([nodeMap(:);edgeMap(:)]); w = zeros(nParams,1); % Compute sufficient statistics suffStat = UGM_MRF_computeSuffStat(y,nodeMap,edgeMap,edgeStruct); % Optimize w = minFunc(@UGM_MRF_NLL,w,[],nInstances,suffStat,nodeMap,edgeMap,edgeStruct,@UGM_Infer_Chain) Iteration FunEvals Step Length Function Val Opt Cond 1 2 7.12949e-05 1.89092e+04 2.96046e+03 2 3 1.00000e+00 1.85021e+04 1.36128e+03 3 4 1.00000e+00 1.80446e+04 1.60027e+03 4 5 1.00000e+00 1.78524e+04 1.07821e+03 5 6 1.00000e+00 1.78029e+04 2.56363e+02 6 7 1.00000e+00 1.78007e+04 4.49694e+01 7 8 1.00000e+00 1.78006e+04 4.37522e+01 8 9 1.00000e+00 1.77998e+04 7.82306e+01 9 10 1.00000e+00 1.77989e+04 1.03849e+02 10 11 1.00000e+00 1.77981e+04 6.17314e+01 11 12 1.00000e+00 1.77979e+04 1.36103e+01 12 13 1.00000e+00 1.77979e+04 6.93718e+00 13 14 1.00000e+00 1.77979e+04 1.28554e+01 14 15 1.00000e+00 1.77979e+04 2.21724e+01 15 16 1.00000e+00 1.77978e+04 2.85041e+01 16 17 1.00000e+00 1.77978e+04 2.28412e+01 17 18 1.00000e+00 1.77977e+04 7.15382e+00 18 19 1.00000e+00 1.77977e+04 8.17118e-01 19 20 1.00000e+00 1.77977e+04 1.84132e-02 20 21 1.00000e+00 1.77977e+04 6.14687e-03 21 22 1.00000e+00 1.77977e+04 2.12248e-05 Directional Derivative below progTol w = -0.2839 0.4308 -0.5626 -0.7103 0.1565
Here are the potentials under this model:


[nodePot,edgePot] = UGM_MRF_makePotentials(w,nodeMap,edgeMap,edgeStruct);
nodePot(1,:)
nodePot(2,:)
edgePot(:,:,1)
ans =

    1.1694    1.0000


ans =

    0.7529    1.0000


ans =

    1.5384    0.5697
    0.4915    1.0000

The likelihood was not noticeably affected by modeling the boundary condition, though the parameters we obtained were significantly different. For example, the potential of the (no rain,no rain) state is now higher than the (rain,rain) state. This illustrates the difficulty in interpreting the potentials, as opposed to looking at marginals obtained via inference or looking at samples from the distribution.

Using the Estimated Parameters

The output of the parameter estimation procedure is a set of parameters w. Subsequently, the UGM_MRF_makePotentials function uses these parameters to make the nodePot and edgePot variables that have been the starting point of all our previous demos. So, after we have finished parameter estimation, we can now consider doing our usual decoding/inference/sampling tasks with our estimated potentials, in the same way that we used our heuristic potentials in the previous demos. For example, we can generate 100 samples from this chain-structured data using:

samples = UGM_Sample_Chain(nodePot,edgePot,edgeStruct);

Below, we show a plot of 100 samples from the model:

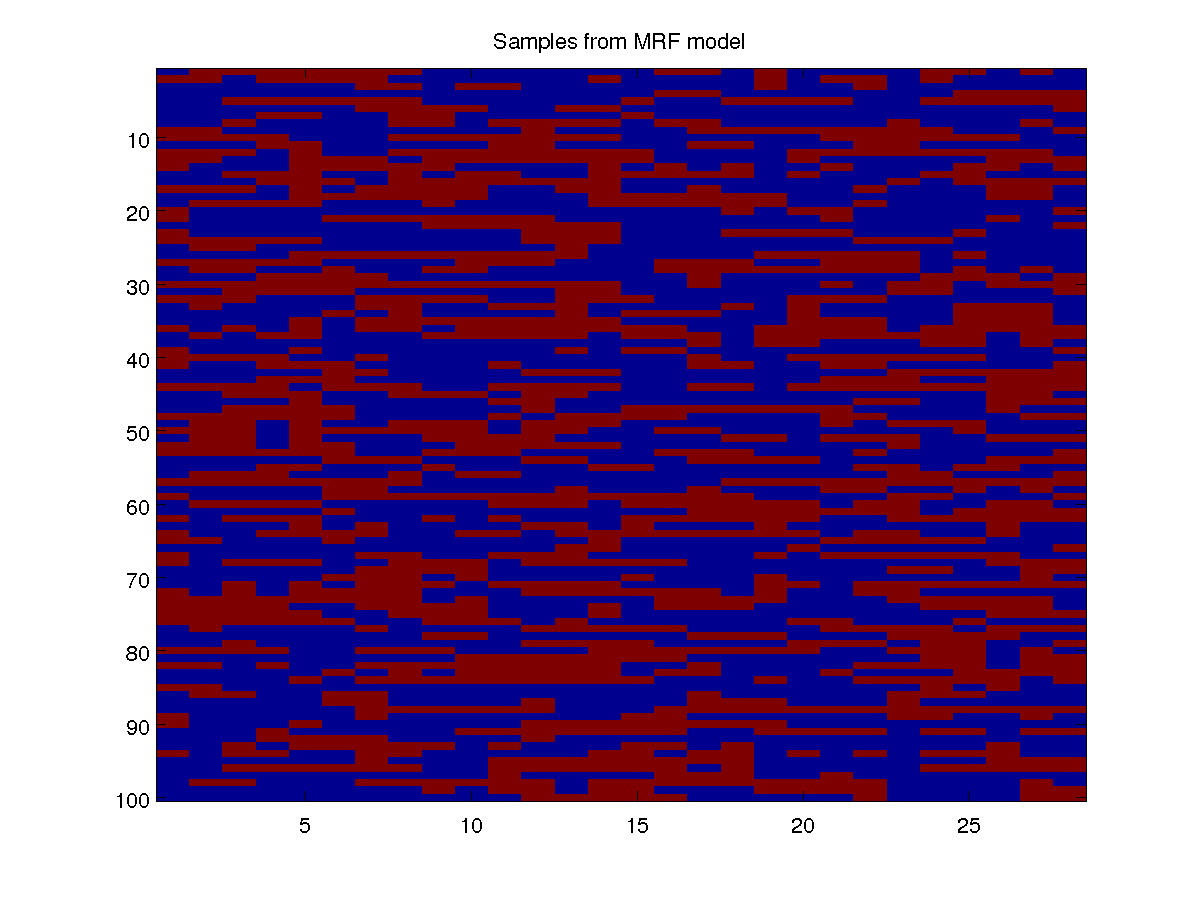
These samples look much more like the real data than the samples from our independent model. Like in the real data, we see long streaks of rainy days, as well as long streaks of days with no rain. Such long streaks are very unlikely under an independent model where the average probability of rain on a random day is 41.15%.

We can just as easily do decoding or inference with the potential functions, as we did in previous demos. Conditional decoding/inference/sampling is also straightforward, and we can use it to try and make predictions given observations. For example, if wee see that it rains on the first days of a month, we can use the model to predict what the rest of the month might look like. Below, we condition on the first two days taking the rain state, and generate 100 conditional samples of the rest of the month:

clamped = zeros(nNodes,1);
clamped(1:2) = 2;
condSamples = UGM_Sample_Conditional(nodePot,edgePot,edgeStruct,clamped,@UGM_Sample_Chain);

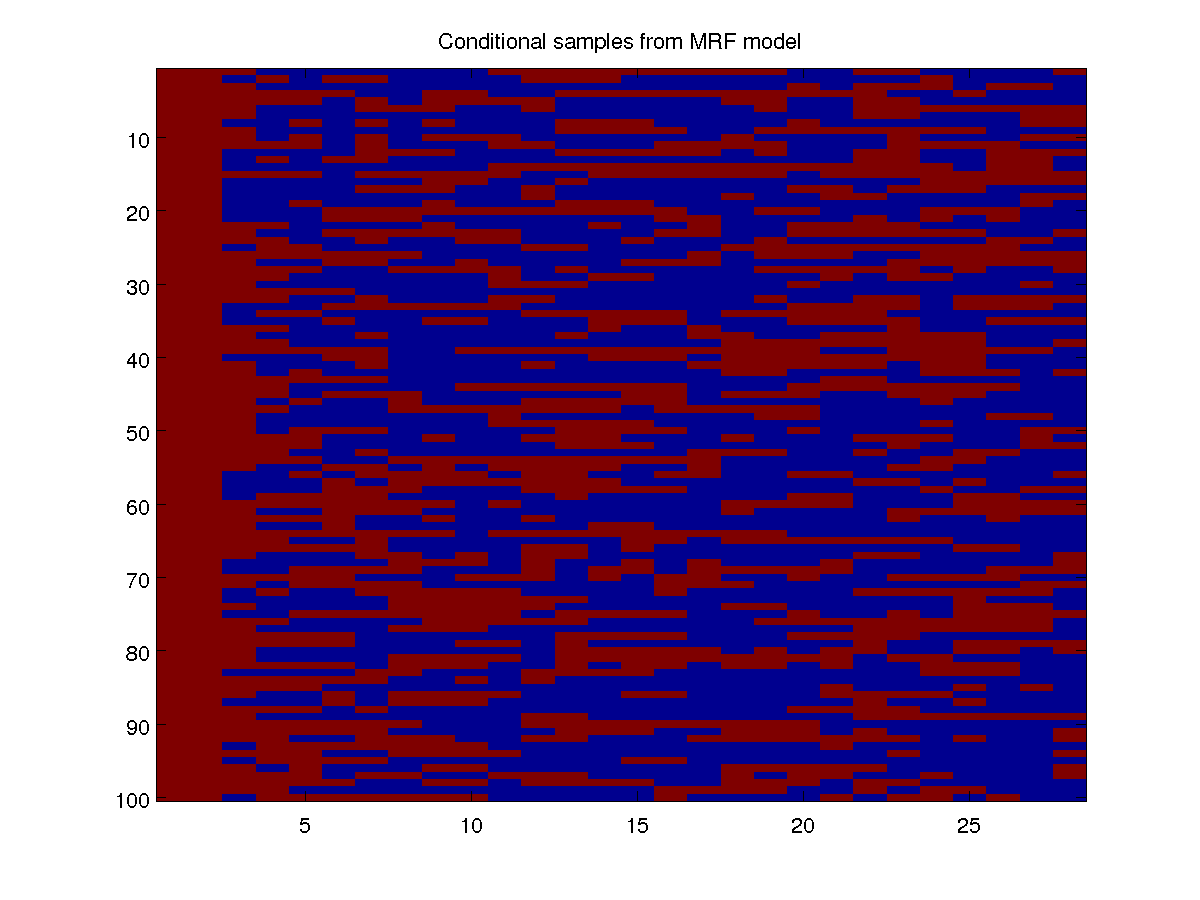
Notes

This demo has focused on the case of chain-structured data. However, as we saw in previous demos, there are many cases where we can perform exact inference. For example, we can also do maximum likelihood parameter estimation with small graphs, trees, forests, and graphs that have a small cutset or treewidth. We just have to change the edgeStruct and inferFunc in order to handle these other types of structures. Since this is straightforward, we will not have separate demos covering these cases.

In the special case of triangulated graphs, also known as decomposable graphical models), the maximum likelihood estimates can be obtained without the need for a gradient method. However, this is not implemented in UGM. Classically, the iterative proportional fitting (IPF) algorithm was used to fit the parameters of MRFs. This method is a form of coordinate descent, but on many problems it is much slower than using L-BFGS (especially for over-parameterized models) so I did not include an implementation of it.

In this and the subsequent demos on parameter estimation, we assume that the graph structure is fixed across training examples. This is why we used the (somewhat ackward) truncation of the rain data to the first 28 days of the month. To use UGM for data sets where different training examples have different graph structures (or number of nodes, number of states, etc.), you simply need to optimizie the sum of the negative log-likelihoods across the examples with different structures.

PREVIOUS DEMO NEXT DEMO

Mark Schmidt > Software > UGM > TrainMRF Demo