Linprog UGM Demo

The problem of computing the optimal decoding can be formulated as a binary integer linear program, and solving this integer program will yield the optimal decoding. Unfortunately, solving integer programs is NP-hard, so I've included the integer programming formulation among the approximate methods because we have no idea how long an integer programming method will take to compute the optimal decoding. For example, below we compute the optimal decoding for problems with 256 nodes using integer programming, but there are problems with 50 nodes that will not be solved in a reasonable amount of time with this technique. After discussing the binary integer linear programming method, we then turn to a linear programming relaxation of this method. Here, we remove the restriction that the solution is integral, leading to a linear program that can be solved in polynomial time to give an approximate decoding.

By default, if it is found on the path, the functions in this demo will cal the GNU Linear Programming Kit (GLPK) to solve the integer/linear programs. If GLPK is not found, Matlab's Optimization Toolbox will be used.

Interger Programming

Rather than searching for the configuration maximizing the joint potential, the integer programming formulation considers the equivalent problem of minimizing the negative logarithm of the joint potential. If we introduce a {0,1} indicator variable for each possible assignment of states to each node and each edge (along with constraints to ensure that these indicator variables are consistent on the edges), then decoding can be written as a binary integer linear program in terms of these variables. In UGM, we can use the integer programming formulation for decoding using: 
getNoisyXsmall
intProgDecoding = UGM_Decode_IntProg(nodePot,edgePot,edgeStruct);

Linear Programming

Unfortunately, finding the optimal decoding using integer programming may be too slow on some problems. However, we can obtain a polynomial-time approximate decoding by relaxing the integer constraints. In particular, rather than enforcing the solution be in the set {0,1}, we enforce that it is in the interval [0,1]. This makes all the constraints linear, so combined with the linear objective function this becomes a linear program.

The linear programming relaxation may not always yield integer solutions. However, it is known that whenever some part of the solution is an integer, that part of the solution must be part of an optimal decoding. Further, ignoring the issue of ties, the entire solution will be integers for tree-structured UGMs and binary UGMs with attractive potentials (as well as some other special cases). When the solution contains fractional solutions, we must use a rounding procedure to obtain a valid discrete decoding.

In UGM, we can use the linear programming relaxation for approximate decoding (with a randomized rounding procedure) using: 

linProgDecoding = UGM_Decode_LinProg(nodePot,edgePot,edgeStruct);
My implementations of the integer/linear programming methods run out of memory if applied to the full noisy X problem. Below, we plot the results of ICM and the integer/linear programming methods applied to one quadrant of the noisy X problem:





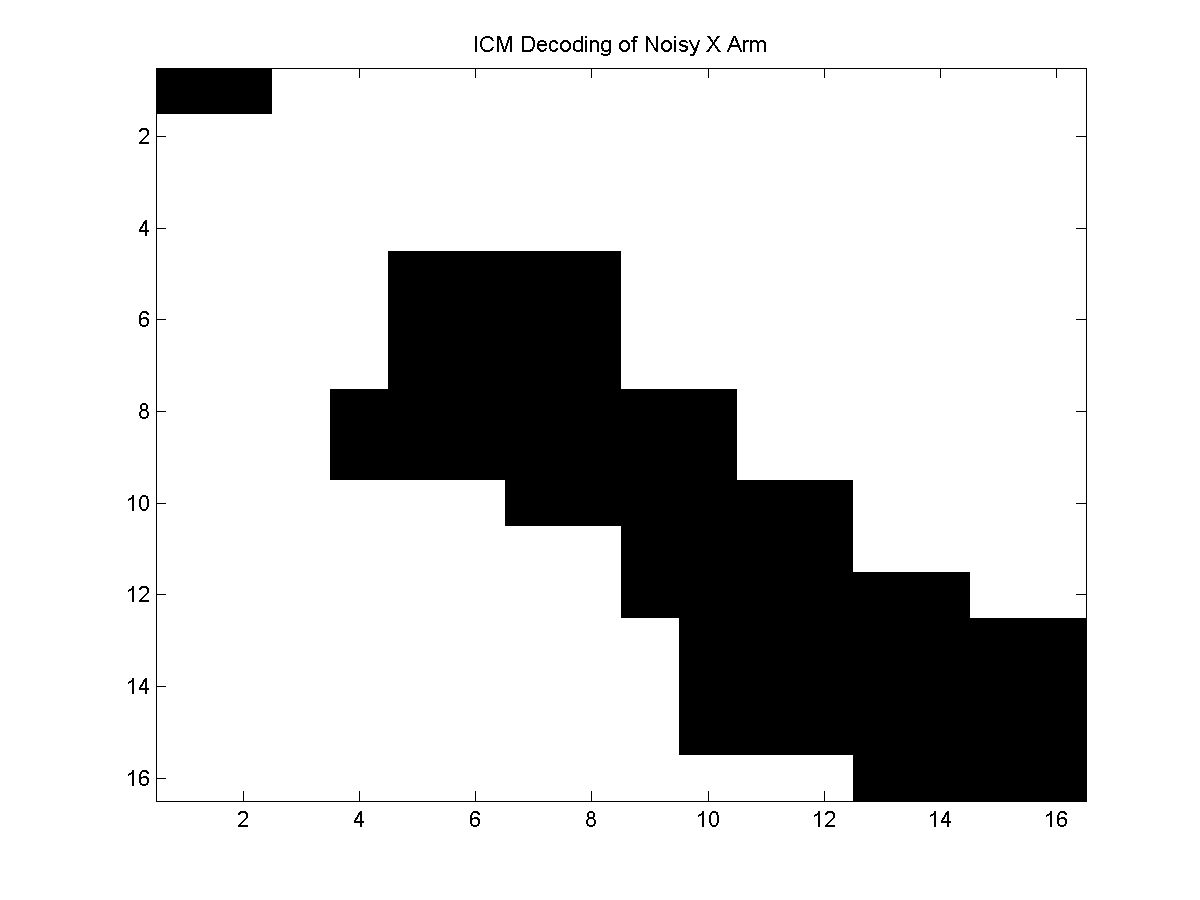
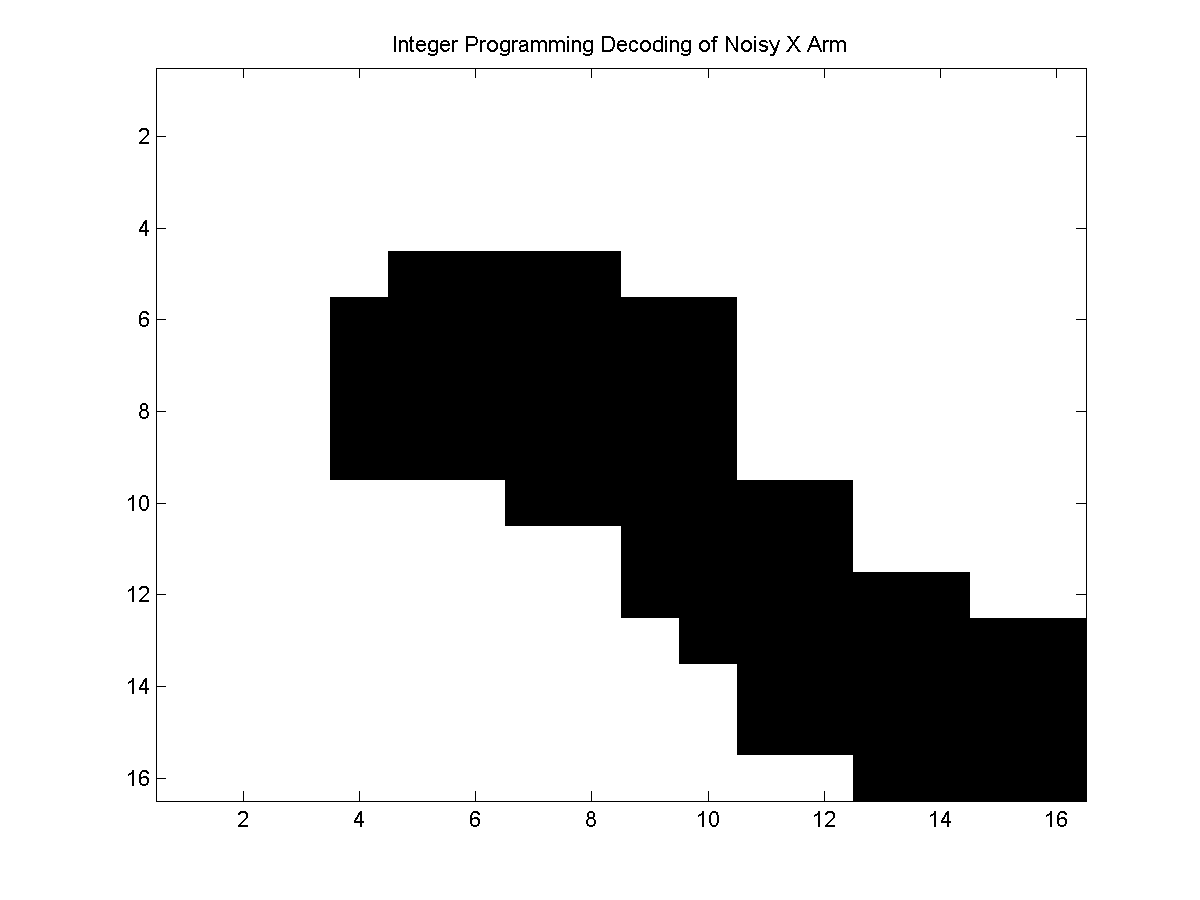
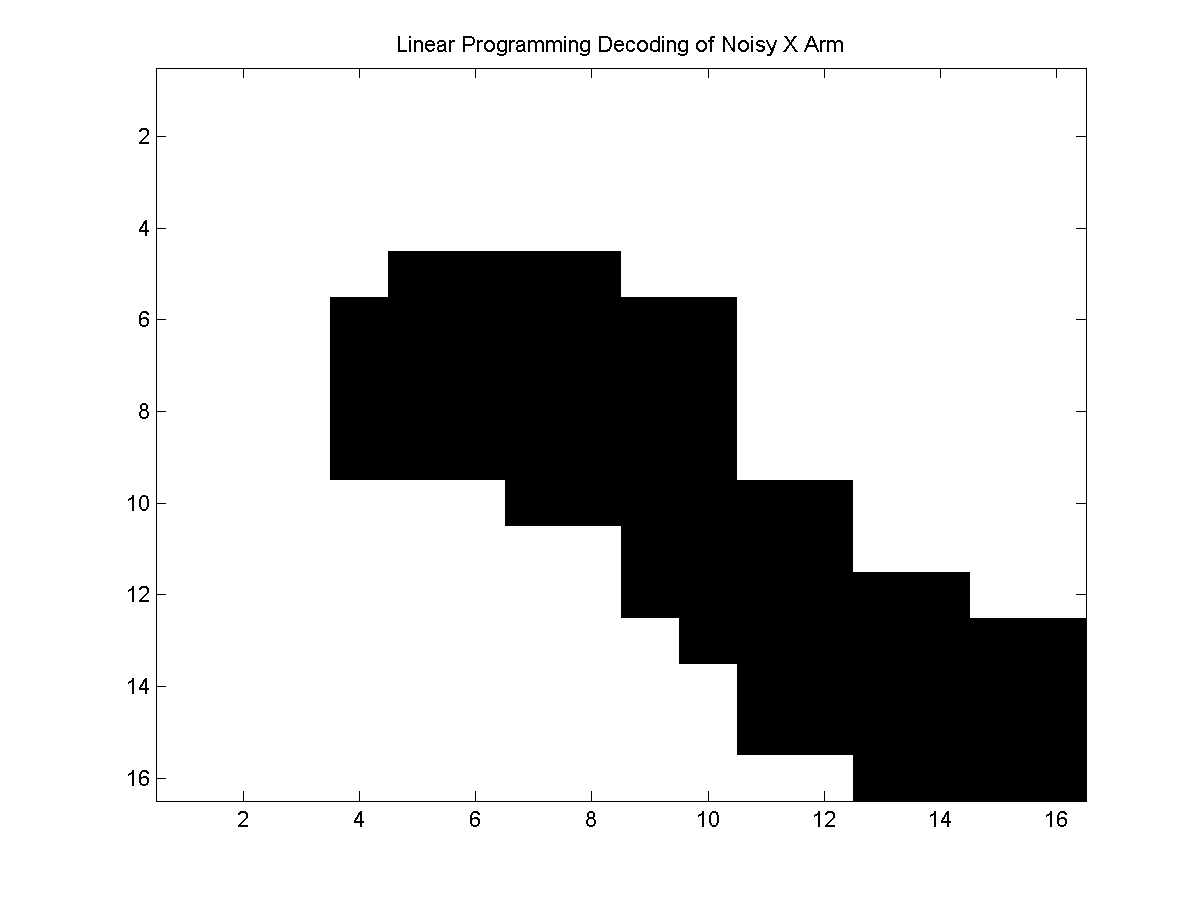
In this case, the integer and linear programming methods give the same (optimal) solution, because the problem is binary and the potentials are attractive. In general, the linear programming method may not find the optimal solution, while the integer programming method may not finish.

Notes

Although the current implementations do not allow us to apply these methods to very large graphs, we could do this if we used a more efficient representation of the constraints.

The linear programming relaxation is one example of a convex relaxation of the problem of finding the optimal decoding. It is possible to use additional linear, cone, and semi-definite matrix constraints to obtain a better approximation. For more information on the integer/linear programming relaxations and these extensions, see:

PREVIOUS DEMO NEXT DEMO
Mark Schmidt > Software > UGM > Linprog Demo