AlphaBeta UGM Demo

In the last demo we saw the block ICM algorithm, an approximate decoding method that works by finding the optimal assignments of an entire block of nodes, given the values of all other nodes. In that demo, we assumed that the blocks formed trees, allowing us to do exact decoding within the block. In this demo, we consider variants where the blocks are defined dynamically so that the blocks are binary with attractive potentials, allowing us to do exact decoding within blocks via graph cuts.

Colored Noisy X

In the case of binary variables, the conditions needed to use the algorithms referred to in this demo reduce to the attractive condition on the edge potentials, and the only possible update reduces to computing the optimal decoding with graph cuts. Because of this, we need to consider a non-binary UGM. We will consider a non-binary version of the noisy X problem.

First, we divide the X into 3 parts, and assign a different primary color to each part. We then corrupt the RGB channels with independent Gaussian noise to make a colored noisy X. We then fit a CRF with a pseudo-likelihood approximation subject to relevant constraints that will allow us to apply the algorithms discussed in this section (we discuss these operations in more detail in a later demo). This is implemented by the function:

getNoisyX2

Below is an example of the colored X and a noisy version of it:

Alpha-Beta Swap Moves

Consider a variant of block ICM where a block is the set all nodes assigned to some state alpha and a second state beta. In general, we won't be able to implement the exact ICM update for this block because the graph structure in the conditional UGM may be arbitrary. However, consider the assumption that we have ep(alpha,alpha)*ep(beta,beta) >= ep(alpha,beta)*ep(beta,alpha) for every edge. Under this condition, we can find the optimal decoding of the block, among the two states. This is referred to as an alpha-beta swap move, since it consists of finding the optimal way to swap states between variables currently labled alpha or beta. The alpha-beta swap moves are typically used in a local search framework, where we iterate through all possible choices of alpha and beta. This is repeated until we find a local optimum where no alpha-beta swap can improve the decoding.

In the previous demo, we discussed the relative 'strengths' of the local optima found by ICM, block ICM, and graph cuts. Performing alpha-beta swaps until we reach a local optima yields another characterization of a local optima: the solution found by the alpha-beta swap moves can not be improved by changing any combination of nodes, restricted to combinations where all nodes are assigned to only 2 of the states. Thus, alpha-beta swap moves find a stronger local optima than ICM, and for binary models they find a stronger local optimum than block ICM. For non-binary models, we will not generally be able to compare the strengths of the optima found by block ICM and alpha-beta swaps.

To use the alpha-beta swap local search method in UGM, we can use:

alphaBetaDecode = UGM_Decode_AlphaBetaSwap(nodePot,edgePot,edgeStruct,@UGM_Decode_GraphCut);

Below, we plot the results for a sample of the colored noisy X problem. The first plot shows the approximate decoding found by ICM, while the next two plots show the approximate decoding found by block ICM and alpha-beta swaps (where we initialize these two with the ICM decoding).

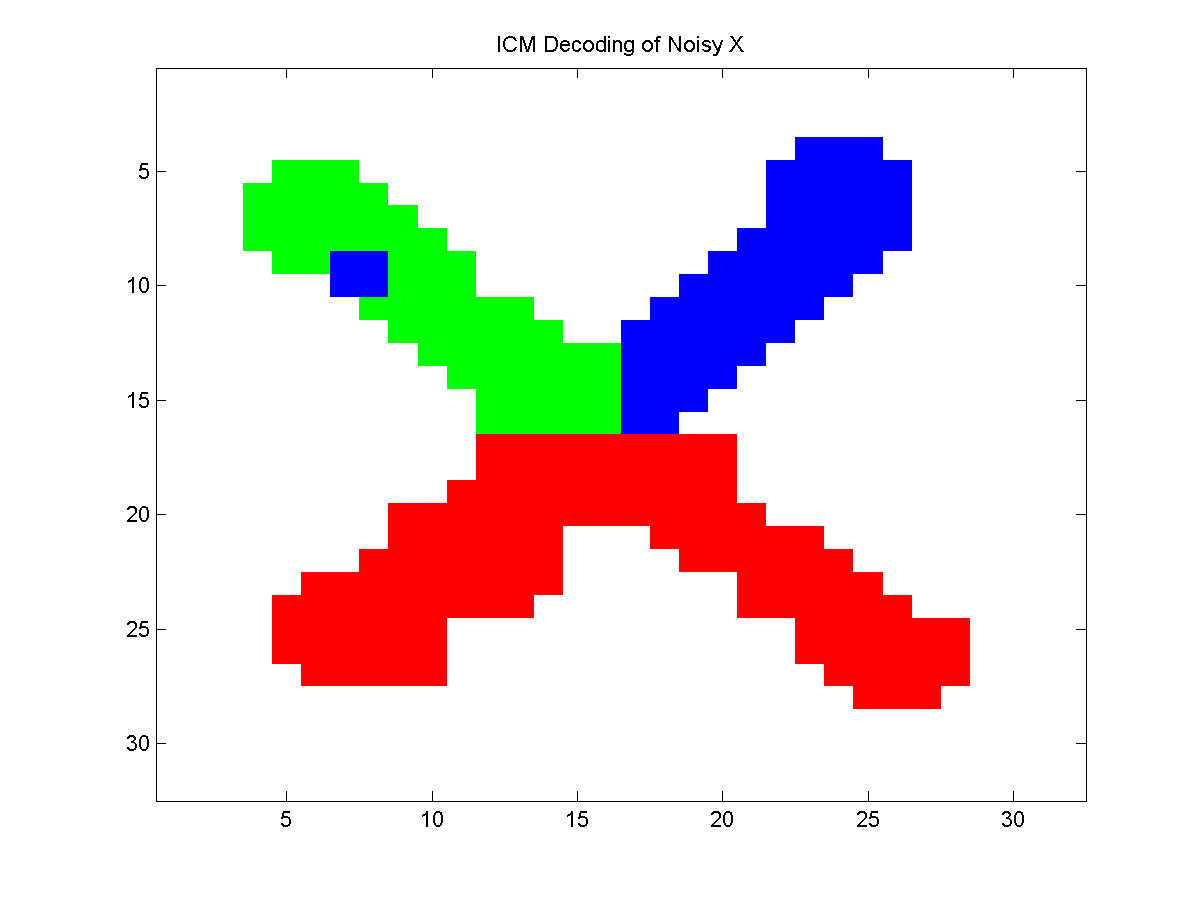
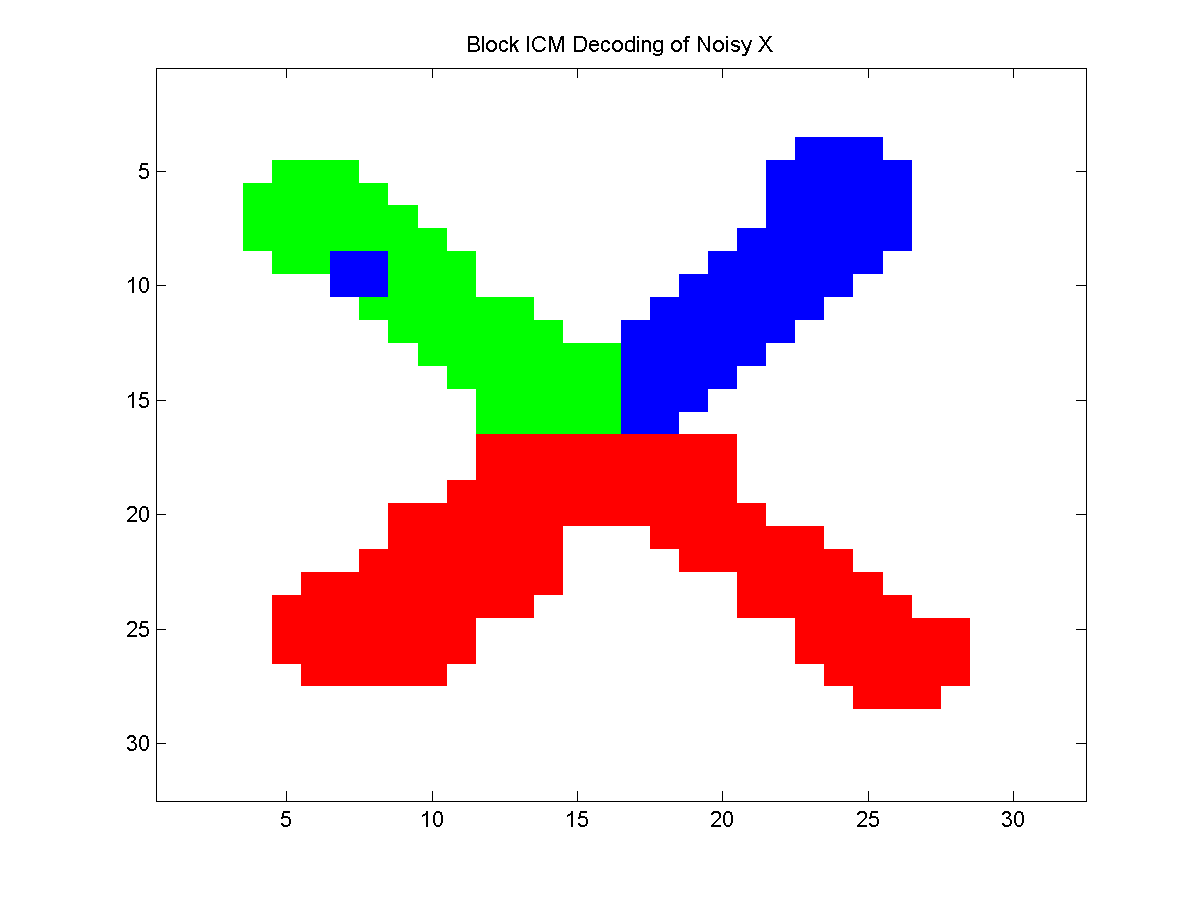
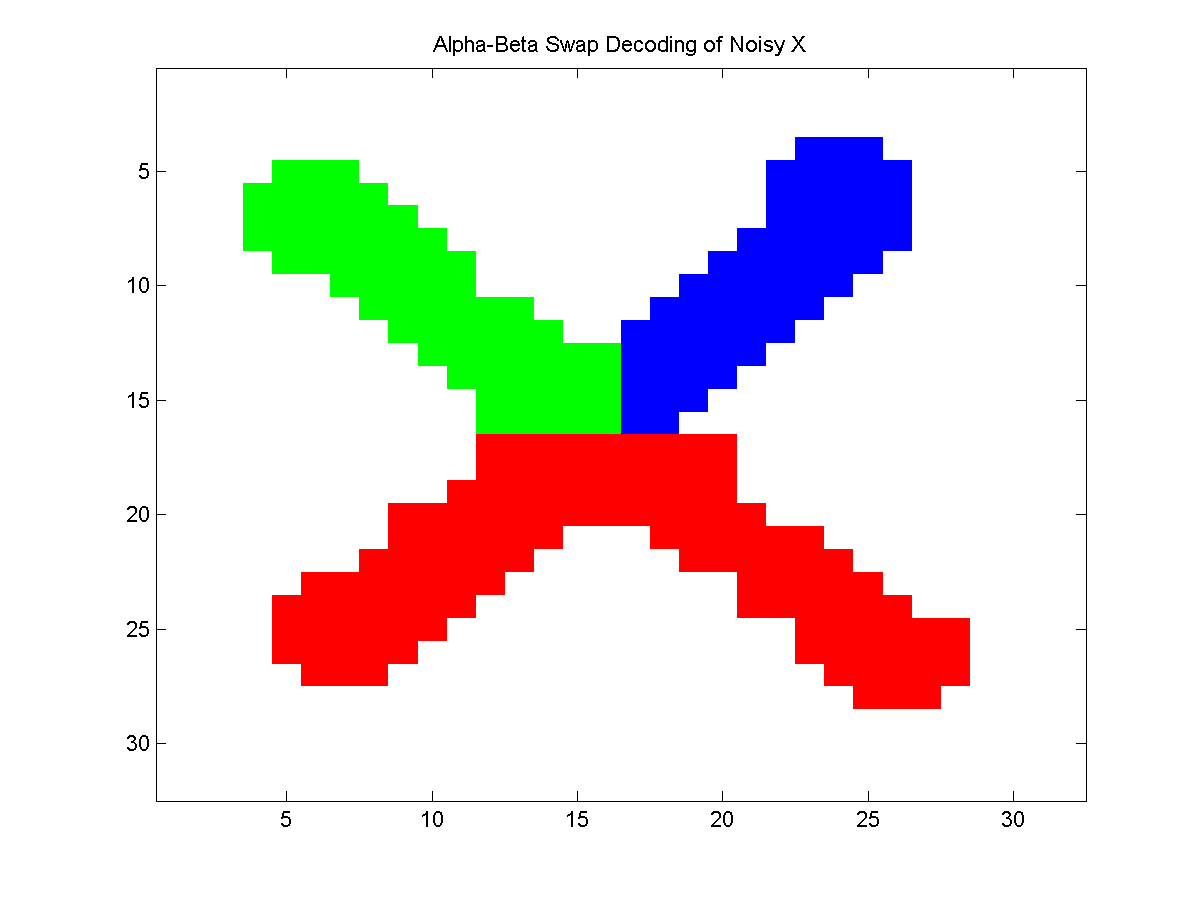
Notice that the block ICM algorithm was not able to remove the misclassified block of pixels in the upper-left arm, but that the alpha-beta swaps fixed this. Of course, the block ICM method could also fix this if we added a suitably constructed block.

Alpha-Expansion Moves

A set of moves that are closely-related to alpha-beta swap moves are alpha-expansion moves. In alpha-expansion moves we choose a state alpha, and we can replace any node's label with alpha. That is, the move consists of 'expanding' the set of nodes labeled alpha. While alpha-beta swap moves rely on the condition ep(alpha,alpha)*ep(beta,beta) >= ep(alpha,beta)*ep(beta,alpha) holding for all edges and all combintaions of states alpha and beta, alpha-expansions rely on the stronger condition that ep(alpha,alpha)*ep(gamma_1,gamma_2) >= ep(alpha,gamma_2)*ep(gamma_1,alpha) for all triplets of states alpha, gamma_1, and gamma_2. However, when this condition is satisfied, alpha-expansions often lead to a substantially better local optimum.

To use alpha-expansions for decoding, we can use:

alphaExpDecode = UGM_Decode_AlphaExpansion(nodePot,edgePot,edgeStruct,@UGM_Decode_GraphCut);

Alpha-Expansion Beta-Shrink Moves

Alpha-expansion moves often lead to better performance than alpha-beta swap moves. But, local optima with respect to alpha-expansions are not necessarily stronger than local optimal with respect to alpha-beta swaps (nor is the converse true). However, we can define a generalization of both moves, alpha-expansion beta-shrink moves, that finds local optima in a stronger sense than both methods. These moves rely on the same conditions as alpha-expansions, and allow us to replace the label of any node labeled alpha with the label beta, and the label of any other node with the label alpha.

To use alpha-expansion beta-shrink moves for decoding, we can use:

betaSelect = 3;
alphaExpBetaShrinkDecode = UGM_Decode_AlphaExpansionBetaShrink(nodePot,edgePot,edgeStruct,@UGM_Decode_GraphCut,betaSelect,ICMDecoding);

Setting betaSelect to 3 iterates through all O(n^2) combinations of alpha and beta, but other options for this variable are available. For example, setting betaSelect to 5 sets beta to alpha+1, which prematurely expands the next value of alpha in the region occupied by the current value.

Notes

Provided that the UGM_Decode_GraphCut code is used for decoding the blocks, the performance of the methods discussed in this demo will be substantially improved if the mex wrapper to the maxflow code is available on the Matlab path.

At this point, we are left with a somewhat unsatisfying answer as to which greedy decoding method works the best. This is because we don't know whether block ICM or alpha-expansion beta-shrink moves will give a stronger local optima. Fortunately, there is an easy solution to this. We could simply alternate between block ICM and alpha-expansion beta-shrink moves until neither can make any improvements. This leads to a combined algorithm that reaches a local optimum in a stronger sense than either algorithm alone. Further, we could augment this algorithm with random restarts (or other stochastic local search tricks) if we want to ensure that the method will eventually find the global optimum.

The alpha-beta swap and alpha-expansion moves originated in the computer vision community, where the required assumptions are often satisfied. In particular, they are discussed in:

Boykov Veksler Zabih (2001). Fast Approximate Energy Minimization via Graph Cuts. IEEE Transactions of Pattern Analysis and Machine Intelligence.

Tthe alpha-expansion beta-shrink moves are proposed in the paper:

Leichter (2009). The Swap and Expansion Moves Revisited and Fused. International Conference on Computer Vision.

In many problems the conditions need to use alpha-expansion moves are not satisfied. One way to apply these moves in these situations is by minimally modifying the energy to make them satisfied, but doing so in such a way that the block update will not decrease the energy. This is described in

Rother Kumar Kolmogorov Blake (2005). Digital Tapestry. IEEE Conference on Computer Vision and Pattern Recognition.

The alpha-expansion and alpha-expansion beta-shrink moves in UGM implement such a strategy, so they can be applied for approximate decoding in general UGMs.

In some applications the edge potentials are identical across edges, up to multiplying their logarithm by a constant. The code available here includes more efficient implementations of the methods discussed in this demo for this scenario.

PREVIOUS DEMO NEXT DEMO

Mark Schmidt > Software > UGM > AlphaBeta Demo