alphaBeta

By Mark Schmidt and Karteek Alahari (2011)
Last updated 19 July 2011.

Summary

The alphaBeta code implements the alpha-expansion beta-shrink moves and other methods for approximate energy minimization described in the paper:

Generalized Fast Approximate Energy Minimization via Graph Cuts: Alpha-Expansion Beta-Shrink Moves
M. Schmidt, K. Alahari.
UAI'11

Clicking on the image below opens a poster giving an overview of the method and results:

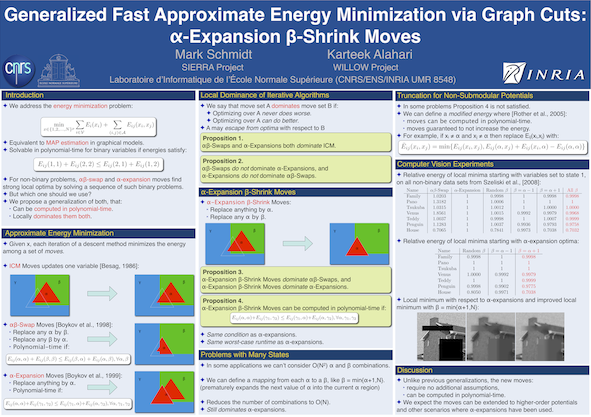
The code contains implementations of several available methods for the problem of computing an approximate minimizer of the sum of a set of unary and pairwise real-valued functions over discrete variables:

min_x: sum_i E_i(x_i) + sum_ij E_ij(x_i,x_j),

where the second sum is over a set of edges in a graph. This equivalent to the problem of MAP estimation, also known as decoding, in a pairwise undirected graphical model.

The particular methods contained in the package are:

iterated conditional mode (ICM): at each iteration, this method finds the optimal update for a single variable.
alpha-beta swap: at each iteration, this method finds the optimal way to swap the labels of all variables assigned to two of the states.
alpha-expansion: at each iteration, this method finds the optimal way to expand the set of variables assigned to one state.
alpha-expansion beta-shrink: at each iteration, this method finds the optimal way to expand the set of variables assigned to one state (alpha-expansion) and to replace the variables that currently have that state with another state (beta-shrink).

The ICM method requires no assumptions on the energies, but the others assume that the pairwise functions encourage the neighbors to take the same state, in the sense that

E_ij(alpha,alpha) + E_ij(beta,beta) <= E_ij(alpha,beta) + E_ij(beta,alpha),

for all edges ij and all pairs of states alpha and beta.

In order to guarantee that they find the optimal move, the two alpha-expansion methods require the stronger condition

E_ij(alpha,alpha) + E_ij(gamma_1,gamma_2) <= E_ij(alpha,gamma_2) + E_ij(gamma_2,alpha),

for all edges ij and all triplets of states alpha, gamma_1, and gamma_2. However, for iterations where this is not satisfied the implementations use a truncation of the energies. See the paper/poster linked above for more details on the problem/methods, and the paper for a list of references.

Download and Examples

To use the code, download and unzip alphaBeta.zip. To solve the binary energy minimization problems, you will also need to have the mex wrapper to the maxflow code installed in a subfolder of this directory.

Once this is done, type the following in Matlab:

>> cd alphaBeta            % Change to the unzipped directory
>> addpath(genpath(pwd))   % Add all sub-directories to the path
>> example_alphaBeta_UGMep % Run the demo with the UGMep code
>> example_alphaBeta_UGM   % Run the demo with the UGM code

Typing the above commands will load the graph and energy function associated with a stereo vision data set, and apply various solvers to it (first with the UGMep implementations, and then with the UGM implementations).

We have included mex files for several operating systems. To compile the mex files for other operating systems, run the included mexAll function.

UGM vs. UGMep

There are two versions of each method available. The UGMep code works directly with node and edge energies and assumes that the edge energies are the same across edges except for multiplication by a scalar. In contrast, the UGM code works with potentials (i.e. pot_i(x_i) = exp(-E_i(x_i))) and allows arbitrary (non-negative) edge potentials on each edge. Thus, the UGMep code is slightly faster and requires substantially less memory if the graph is sparse, but the UGM code allows more general edge energies.

Note that the full UGM package as well as some introductory material on undirected graphical models is available here.

Mark Schmidt > Software > alphaBeta