CS 542D, Term 1, Winter 2004-2005 Class Home Page

Level Set Methods

Dynamic Implicit Surfaces and the Hamilton-Jacobi Equation

Contents of this page

Late breaking news
Things to print
- Handouts
- Homeworks
Course Overview
Course Details
Tentative Schedule
Course Projects
Related Links

Growing Set: avi mpg
Final Set: avi mpg

Late Breaking News:

2004/12/10: Final project reports are due at 12:00 noon on Friday December 17. Email a pdf version to the instructor (with your login name as the filename).
2004/11/28: Project presentation assessment form is available below in the Handouts section.
2004/11/17: Sign up sheet for project presentations is posted on my office door. All students registered in the class must sign up for a 10 minute slot.
2004/11/17: The midterm and solutions are posted in the Homework section below. Midterms may be picked up in person from me.
2004/11/17: Homework #3 may be picked up outside my office. Solutions are posted below.
2004/11/08: Solutions to Homework #4, question #3 is available below.
2004/11/08: I will try to be in or near my office from 1pm - 4pm Monday November 8 and 3pm - 5pm Tuesday November 9 to answer questions regarding the midterm. You may also arrange specific times via email.
2004/11/01: Homework #4, question #3 is due in class on November 8 with no exceptions. This will allow me to release solutions that afternoon in advance of the midterm. The other two questions may be turned in according to the normal policy.
2004/10/31: Solutions for Homework #2 are available below.
2004/10/28: Slides for lectures 13 & 14 are posted below.
2004/10/22: Homework #4 is available below.
2004/10/20: Homework #3, question #3 is now a bonus question.
2004/10/15: Homework #3, question #2 has been modified to remove the time dependence of the flow field. You can find a sample of the expected output in the homework section below.
2004/10/12: Test image for homework #3, question #1 is available below. All formats (png, tiff, bmp) are the same image. Or you can generate the image yourself using the testImage.m file; however, note that you may have to flip the resulting array (using fliplr) to get the image right.
2004/10/11: Solution and discussion of selected components of homework #1 is now available below.
2004/10/06: Project description handout is available below, or copies can be picked up from outside the professor's office. Handout containing some ideas for projects can be picked up from the professor's office.
2004/10/06: Homework #3 available below.
2004/10/04: Office hours 12:30 - 2pm today.
2004/09/29: Course schedule has been updated to account for previous lectures and to show estimates for next two weeks.
2004/09/23: Two talks of interest to our community today: Zoran Popovic from University of Washington on "Control Problems in Computer Graphics" (including fluid flow) at Scarfe 203 from 2pm - 3pm and Peter Schroder from Caltech on "Discrete Differential Geometry" at Ampel 311 from 4pm - 5pm.
2004/09/22: Second homework is available.
2004/08/10: The first lecture will be held on Monday, September 13, 2004.

Handouts

#	Date	Topic
1	Friday, Sept. 10	List of likely course topics.
2	Wednesday, Oct. 6	Description of course project. A list of potential projects is available from the professor.
3	Monday, Nov. 29	Assessment form for project presentations.

Homeworks

Homework Submission Policy:

Get it in soon or I can't release solutions.
Get it in by the end of the semester, or you won't get a grade.

#	Due Date	Assignment	Solution	Other Files
1	September 22	Problem Set	Solutions	none
2	October 6	Problem Set	Solutions	none
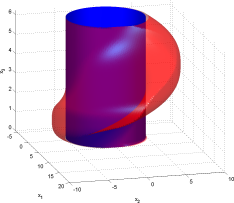
3	October 20	Problem Set	Solutions	testImage.png, testImage.bmp, testImage.tiff, Matlab image generation routine. Expected reach set for question #2.
4	November 8	Problem Set	Solutions	none
*	*	Midterm	Solutions	Mean 48.4, Standard Deviation 8, Median 50, Maximum 60.5, Minimum 35.5

Course Overview

Level set methods are a class of numerical algorithms for simulation of dynamic implicit surfaces and approximation of solutions to the Hamilton-Jacobi (HJ) partial differential equation (PDE).

Dynamic implicit surfaces prove useful in such fields as:

Computational Geometry and Mesh Generation.
Fluid and Combustion Simulation.
Graphics and Animation.
Image Processing and Computer Vision.

The benefits of an implicit representation of surfaces include hassle free merging and separation of surfaces, easy computation of geometric properties like normals and curvature, and the fact that both curves in two dimensions and surfaces in three dimensions can be treated with the same theory and computational algorithms.

The course will begin with an examination of numerical methods for computing dynamically evolving implicit surfaces. Students will experiment in Matlab with state-of-the-art high order accuracy methods using a Toolbox of Level Set Methods developed by the instructor, and will therefore be able to progress rapidly to application specific details from the fields mentioned above.

The second part of the class will turn to the HJ PDE, which arises in such fields as:

Dynamic Programming.
Financial Mathematics and Mathematical Ecology (through Stochastic Differential Equations).
Robotics and Optimal Control.
Verification and Reachable Sets.
Zero-Sum Differential Games.

This component will examine generalizations of the level set methods mentioned above, as well as other classes of algorithms (including fast marching, ordered upwind, and sweeping) and some of the viscosity solution theory underlying this ubiquitous equation. Applications will be explored depending on students' interests.

In addition to attending lectures, students will be expected to:

Read and discuss academic papers.
Complete several homework assignments involving both paper and pencil and programming components.
Complete a course project (which may be tailored to each student's own research or interests).

Course Details

Intended Audience: Graduate students in

Computer Science,
Applied Mathematics,
Engineering and other application fields.

Prerequisites: None officially.

Students should have seen elementary differential equations, multivariable calculus and introductory numerical methods.
Be ready to program. Homework assignments will most easily be solved with Matlab. Programming in Matlab is essentially the same as Java or C but with lots of useful visualization tools. Course projects may be programmed in the language of the student's choosing, should programming be required.
Familiarity with numerical methods for partial differential equations is not necessary.
If you are in doubt, come to the first class or see me.

Instructor: Ian Mitchell

Email: mitchell (at) cs (dot) ubc (dot) ca
Office Location: CISR/CS 233
Office Phone: (604) 822-2317
Office Hours: TBA (and by appointment)

Lectures: 11 - 12:30, Mondays and Wednesdays, Forest Sciences Center (FSC) 1002

Location is subject to change; check here or the CS Graduate Course web page for updates.
There is no lecture Monday September 6 (Labour Day Holiday).
There is no lecture Wednesday September 8 (cancelled for CS orientation).
There is no lecture Monday October 11 (Thanksgiving Holiday).

References:

Level Set Methods and Dynamic Implicit Surface by Stanley Osher and Ronald Fedkiw. The official (required) textbook for the class, available at the bookstore. Excellent coverage of high order accuracy methods on structured grids, image processing and computational physics.
Level Set Methods and Fast Marching Methods by James Sethian. The other level set book. Excellent coverage of fast marching methods, unstructured grids, and many other applications. Inexpensive.
A Toolbox of Level Set Methods by Ian M. Mitchell. The manual for the Matlab Toolbox used in the course.
Research papers listed (and linked) in the Schedule below.

Grades: Your final grade will be based on a combination of

3-5 homework assignments,
1 midterm,
in class project presentation,
written project report.

The relative weighting will depend on how many homework assignments I come up with.

Other References:

Numerical Analysis by Burden and Faires.
Scientific Computing: An Introductory Survey by Heath.
Elementary Differential Equations and Boundary Value Problems by Boyce and DiPrima.
Single Variable Calculus and Calculus of Several Variables by Adams.
Partial Differential Equations by L. C. Evans.
Finite Difference Schemes and Partial Differential Equations by Strikwerda.
Finite Volume Methods for Hyperbolic Problems by LeVeque.
Curves and Surfaces for Computer Aided Geometric Design by Farin.
Geometric and Solid Modeling: An Introduction by Hoffmann.

The Schedule:

Topics of future lectures are subject to change.
Some readings and/or links may not be operational from computers outside the UBC domain. If you have problems, please contact the instructor.
Readings marked "OF" are from the Osher and Fedkiw text, "S" are from the Sethian text, and "T" are from the Toolbox Manual.

#	Date	Topic	Links	Required Readings	Optional Readings
1	Sept 13	Introduction. Surface Representations.	Matlab's Introduction to initial value ODEs (available locally through Matlab's helpdesk command)	none.	Representations: Farin. Hoffmann. ODEs: Boyce & DiPrima chapter 8. Burden & Faires chapter 5. Heath chapter 9.
2	Sept 15	Implicit Surface Functions. Constructive Solid Geometry. Matlab introduction.	Toolbox of Level Set Methods	OF chapter 1	T section 3.3
3	Sept 20	Signed Distance Functions. Computer representation of continuous functions.	none	OF 2	OF 3.3-3.4, Heath 8.6, Burden & Faires 4.1, Strikwerda 1
4	Sept 22	Motion by convective flow. Upwind spatial derivative approximation.	none	OF 3.1-3.2, T 2.1	T 3 (as needed), Heath 11.1-11.2, Burden & Faires 12.2-12.3
5	Sept 27	Temporal derivative approximation. CFL timestep restriction. Multiple dimensional motion.	none	OF 3.2	none
6	Sept 29	High order methods (TVD RK, ENO, WENO). Motion in the normal direction.	none	OF 3.3-3.5	T 2.7.2
7	Oct 4	Motion in the Normal direction. Combinations of Motion. Reinitialization	none	OF 6.1, 6.2, 6.4, T 2.3.2-2.3.3	none
8	Oct 6	Reinitialization Equation. Motion by Mean Curvature. Course Project Discussion.	none	OF 7.1-7.4, 4.1-4.3, T 2.2.1, 2.3.1, 2.4	S 2.3-2.4, 12.1-12.3
	Oct 11	Thanksgiving Holiday (no class)
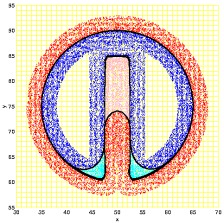
9	Oct 13	Constraints and Masking. Applications: Reach Sets (no inputs), Image Segmentation.	none	OF 12.1, T 2.2.3	S 12.4.3
10	Oct 18	Optimal Control and the Hamilton-Jacobi Bellman equation.	none	none	Evans 10.3
11	Oct 20	General first order HJ terms.	none	OF 5.1, 5.3, T 2.2.2, 2.5	OF 5.2
12	Oct 25	Forcing terms. Differential Games.	none	none	"Differential Games and Representation Formulas for Solutions of Hamilton-Jacobi-Isaacs Equations" by Evans & Souganidis, Indiana U. Math. J., v.33, n.5, pp.773-797 (1984).
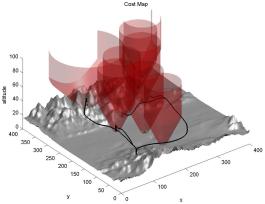
13	Oct 27	Continuous Reach sets (with inputs)	Application of Level Set Methods to Control and Reachability Problems in Continuous and Hybrid Systems by Mitchell. Reach Set Lecture Slides.	T 2.6, section 2.1 of Mitchell	Mitchell 2-3
14	Nov 1	Reach Sets: Projections & Hybrid Systems. Minimum time to reach.	Reach Set Lecture Slides.	none	S 20.1-20.3, Mitchell 4-6
15	Nov 3	Static to Time-Dependent Transformation.	"A Toolbox of Hamilton-Jacobi Solvers for Analysis of Nondeterministic Continuous and Hybrid Systems" by Mitchell & Templeton, submitted to HSCC 2005.	Mitchell & Templeton section 3.	"A Level Set Formulation for the solution of the Dirichlet Problem for Hamilton-Jacobi Equations" by Osher, SIAM J. Math. Anal. v.24, pp. 1145-1152 (1993).
16	Nov 8	Fast Marching	"Efficient algorithms for globally optimal trajectories" by Tsitsiklas. "A fast marching level set method for monotonically advancing fronts" by Sethian.	OF 7.5	S 8
	Nov 10	Midterm exam
17	Nov 15	Path Planning with Fast Marching Method.	Path Planning Slides. "Optimal Algorithm for Shape from Shading and Path Planning" by Kimmel & Sethian. "Continuous Path Planning with Multiple Constraints" by Mitchell & Sastry.	none.	none.
18	Nov 17	Iterative and Sweeping Methods. Velocity Extension.	"Fast Sweeping Algorithms for a Class of Hamilton--Jacobi Equations" by Tsai et. al. "The Fast Construction of Extension Velocities in Level Set Methods" by Adalsteinsson & Sethian.	OF 8	S 11.2-11.4
19	Nov 22	Conservation Laws. Particle Level Set Method.	"Animation and Rendering of Complex Water Surfaces" by Enright, Marschner and Fedkiw. "A Hybrid Particle Level Set Method for Improved Interface Capturing" by Enright et. al. PLS lecture slides.	OF 9	OF 14-21
20	Nov 24	Vector Level Sets. Stochastic Systems and the Kolmogorov Equation. Course Summary	"A Toolbox of Hamilton-Jacobi Solvers for Analysis of Nondeterministic Continuous and Hybrid Systems" by Mitchell & Templeton, submitted to HSCC 2005.	OF 10.1-10.3, Mitchell & Templeton section 4.	none.
21	Nov 29	Project Presentations.
22	Dec 1	Project Presentations.
	Dec 7-21	Exam period. Projects due at noon on Friday, December 17.

Course Projects:

Students enrolled in the course prepared the following projects:

Student	Topic	Title
Eric Brochu	3D Visualization	Implicit Surface Ray Tracer
Tyson Brochu	Faster Time Integration Algorithm	Semi-Lagrangian Time Integration
Wan Chen	Image Segmentation Application	Active Contour Without Edges in Level Set Formulation
Sarah Cormier	Algorithm to Reduce Computational Complexity	A Toolbox Implementation of the Local Level Set Method
Kevin Loken	Algorithm to Reduce Numerical Dissipation	Particle Level Set Method
Zhenguo Pan	New Type of Surface Motion	Level Set Method for Motion by Surface Diffusion
Scott Olsen	Path Planning Application	Level Set Methods Approach to Optimal Path Planning
Tiberiu Popa	Generation of Explicit Surface Representation in 3D	Survey of Triangulation Algorithms of Implicit Function Represented on Regular Grids
Tim Rees	Financial Mathematics Application	A Level Set Approach to a Stochastic Differential Equation in Mathematical Finance
Dana Sharon	Algorithm for Solving the Stationary HJB	Implementation of the Fast Marching Method
Ian Stavness	Surface Reconstruction Application	Reconstruction of Surfaces from Unorganized Data Points
David White	Additional Toolbox Features	Spatial and Time-Dependent Boundary Conditions
Alan Woo	Physically Based Modelling Application	Low-Speed Flame
Yongning Zhu	Adaptive Mesh Refinement	Adaptively Refined Meshes for Level Set Functions

Links:

CS 542D Term 1 Winter 2004-2005 Course Web Page (this page): http://www.cs.ubc.ca/~mitchell/Class/CS542D.2004/index.html
CS 542D is offered by

A few of the many researchers active in level set methods (and their favorite applications, if applicable):
- Ronald Fedkiw (animation and fluids)
- Ben Houston (animation)
- Ron Kimmel (image processing and robotics)
- Stanley Osher (image processing)
- Steve Ruuth (at SFU, PDE solvers)
- James A. Sethian (many different applications)
- Alexander Vladimirksy (control theory and differential games)
- Hong-Kai Zhao (image processing and graphics)

CS 542D Term 1 Winter 2004-2005 Class Page
maintained by Ian Mitchell