TrainSGD UGM Demo

For MRFs, we only need to make one pass through the data to compute sufficient statistics, so the number of training examples does not have a large influence on the time needed for parameter estimation. For CRFs, in general we need to do inference for each training example to evaluate the objective function and gradient. This can make parameter estimation very slow if we have a large number of training examples. If we are happy with a crude approximate solution to the parameter estimation problem, then stochastic gradient descent methods are an appealing alternative to unconstrained optimization techniques, since they do not require exact function evaluations.

Conditional Noisy-X

In the last demo, we only used one training example for the conditional noisy-X problem. Consider now the case where we have many input-output pairs and want to find the best parameters across the images. In particular, we will generate a data set with 100 examples: 
load X.mat
[nRows,nCols] = size(X);
nNodes = nRows*nCols;
nStates = 2;
nInstances = 100;

% Make 100 noisy X instances
y = int32(1+X);
y = reshape(y,[1 1 nNodes]);
y = repmat(y,[nInstances 1 1]);
X = y + randn(size(y))/2;

%% Make edgeStruct

adj = sparse(nNodes,nNodes);

% Add Down Edges
ind = 1:nNodes;
exclude = sub2ind([nRows nCols],repmat(nRows,[1 nCols]),1:nCols); % No Down edge for last row
ind = setdiff(ind,exclude);
adj(sub2ind([nNodes nNodes],ind,ind+1)) = 1;

% Add Right Edges
ind = 1:nNodes;
exclude = sub2ind([nRows nCols],1:nRows,repmat(nCols,[1 nRows])); % No right edge for last column
ind = setdiff(ind,exclude);
adj(sub2ind([nNodes nNodes],ind,ind+nCols)) = 1;

% Add Up/Left Edges
adj = adj+adj';
edgeStruct = UGM_makeEdgeStruct(adj,nStates);
nEdges = edgeStruct.nEdges;
Below, we plot the first four noisy X values.

We make the nodeMap and edgeMap variables as before: 
% Add bias and Standardize Columns
tied = 1;
Xnode = [ones(nInstances,1,nNodes) UGM_standardizeCols(X,tied)];
nNodeFeatures = size(Xnode,2);

% Make nodeMap
nodeMap = zeros(nNodes,nStates,nNodeFeatures,'int32');
for f = 1:nNodeFeatures
    nodeMap(:,1,f) = f;
end

% Make Xedge
sharedFeatures = [1 0];
Xedge = UGM_makeEdgeFeatures(Xnode,edgeStruct.edgeEnds,sharedFeatures);
nEdgeFeatures = size(Xedge,2);

% Make edgeMap
f = max(nodeMap(:));
edgeMap = zeros(nStates,nStates,nEdges,nEdgeFeatures,'int32');
for edgeFeat = 1:nEdgeFeatures
   edgeMap(1,1,:,edgeFeat) = f+edgeFeat;
   edgeMap(2,2,:,edgeFeat) = f+edgeFeat;
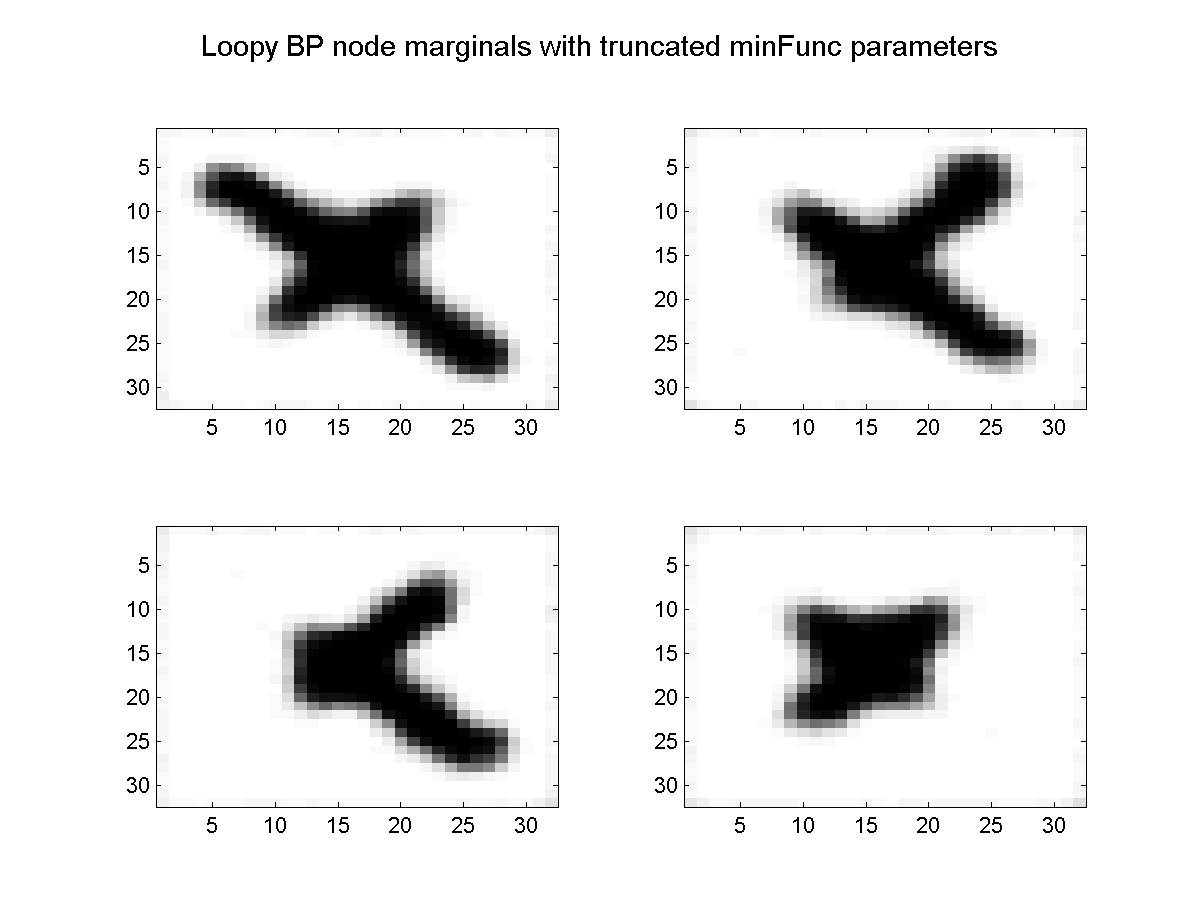
end
We now have 100 images each with 1024 nodes, that we are using to estimate 5 parameters. Given that we could find the optimal parameters in the single-instance case after less than 300 iterations, we might expect that we could find the optimal parameters in the multiple instance case by passing through the 100 image data set 3 times. Below, we plot the marginals obtained after running minFunc for 3 function evaluations (loopy belief propagation was used for inference):

Training with Stochastic Gradient Descent

Unfortunately, minFunc assumes that the function to minimize is a black box, and is not able to take advantage of the large amount of redundancy in the data. In contrast, stochastic gradient descent (SGD) only examines part of the function at a time, so is able to to make more progress. The SGD algorithm is very simple: at each iteration we pick a random training example, evaluate the gradient on that training example, and take a small step in the direction of the negative gradient (the step size is typically fixed at a small constant value, or decreased over time). We give the procedure below: 
maxIter = 3; % Number of passes through the data set
stepSize = 1e-4;
w = zeros(nParams,1);
for iter = 1:maxIter*nInstances
    i = ceil(rand*nInstances);
    funObj = @(w)UGM_CRF_NLL(w,Xnode(i,:,:),Xedge(i,:,:),y(i,:),nodeMap,edgeMap,edgeStruct,@UGM_Infer_LBP);
    [f,g] = funObj(w);
    
    fprintf('Iter = %d of %d (fsub = %f)\n',iter,maxIter,f);
    
    w = w - stepSize*g;
end
Since SGD only looks at a single training example on each iteration, its iterations are much less costly. If we run SGD for 300 iterations (corresponding to the same cost as 3 function evalutions), we obtain the results below:

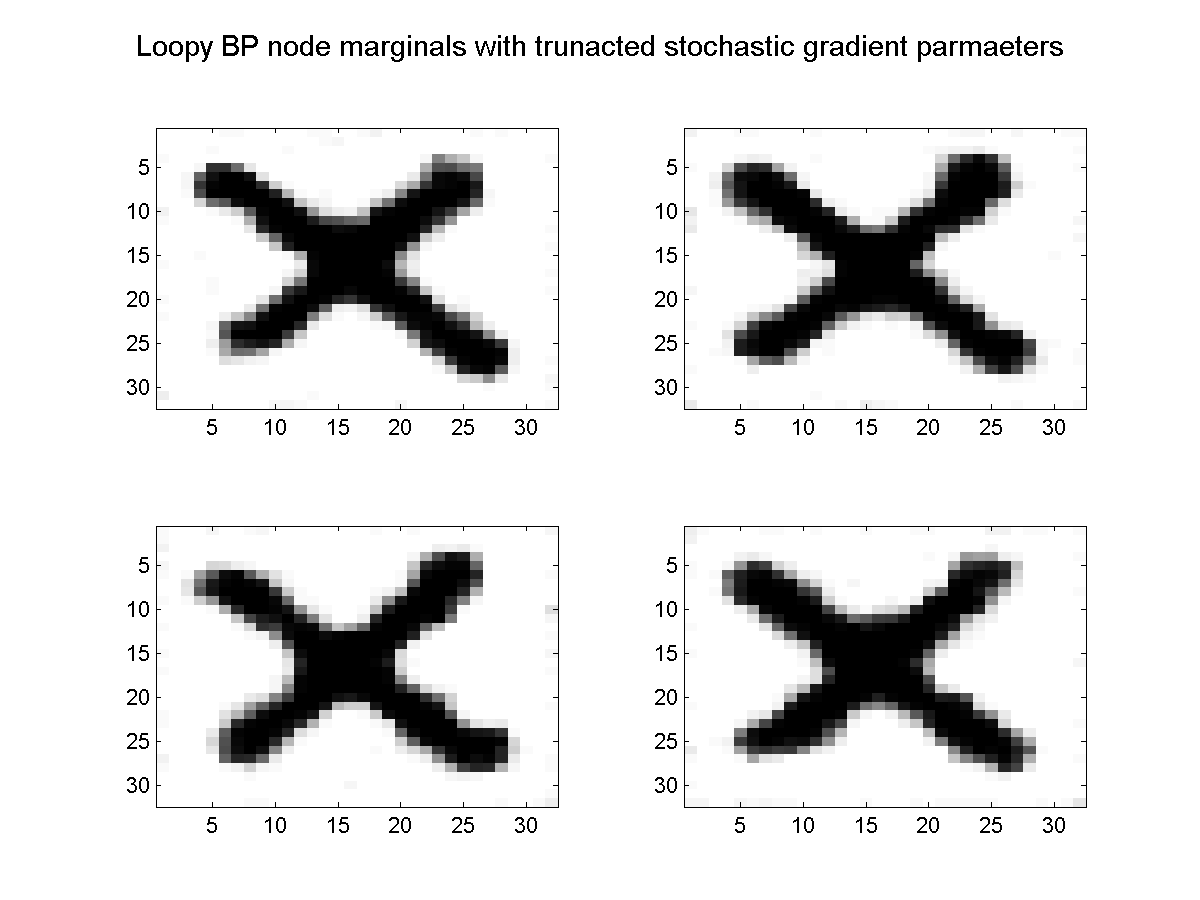
In this case, SGD has obtained a better result in the time-limited setting. If we ran them longer, minFunc would eventually find a better solution and terminate, but the time for minFunc to 'catch up' to the more simple method increases with the size and amount of redundancy in the data set. This makes SGD useful for training CRFs on very large data sets.

Notes

We have given the case of SGD for maximum likelihood estimation above. It is easy to modify SGD to do L2-regularized estimation by replacing the objective with the regularized objective function (using penalizedL2). Similarly, we could enforce the sub-modularity constraint by taking a projected stochastic gradient iteration. In the case of non-negative constraints, this would simply involve setting elements to 0 where they become negative.

We proposed to use SGD for training CRFs in:

Other than having a large number of training examples, several other motivations exist for exploring methods similar to SGD. For example, max-margin Markov networks use an alternative objective function for training conditional UGMs. In these models, evaluating the objective function requires decoding (instead of inference). Thus they can be applied in cases where we can do exact decoding, or can be applied with an approximate decoding method. The below paper examines training max-margin Markov network with stochastic sub-gradient descent: Variants on SGD have also been explored for Markov random fields where an approximate sampling method is used for approximate inference. This has been popularized lately under the name 'contrastive divergence', and dates back to: Despite the appealing properties of SGD that we discuss above, there are several disadvantages to training with SGD: To address these disadvantages, we can consider using an algorithm that starts out using iterations to SGD, but slowly transforms into a deterministic L-BFGS algorithm like minFunc. Motivated mainly by the problem of training CRFs, we proposed a method of this type in the paper: A simple implementation of the method is available here (note that the UGM code included in this package is the older 2009 version).

PREVIOUS DEMO

Mark Schmidt > Software > UGM > TrainSGD Demo