GraphCuts UGM Demo

There are no known exact algorithms for decoding/inference/sampling in UGMs that don't in general require a runtime that is exponential in the treewidth of the graph. However, we can sometimes still do these operations efficiently by considering a restricted class of potentials. In this demo, we consider the case of binary variables with attractive potentials. In this scenario, it is still possible to find the optimal decoding in polynomial time, independent of the graph structure, by re-formulating the problem as a minimum graph-cut problem.

By default, the UGM_Decode_GraphCut function searches for the mex wrapper to the maxflow code. If this software is not found on the path, then UGM_Decode_GraphCut uses a simple implementation of the Ford-Fulkerson method. Note that the Ford-Fulkerson implementation is very slow, so it recommended to install the maxflow software for larger graphs.

Binary Image Denoising Problem

We consider a binary image denoising problem, where we are given a binary image that has been corrupted by independent Gaussian noise, and we want to try to recover the original image. For example, the image below is known as the "famous X":

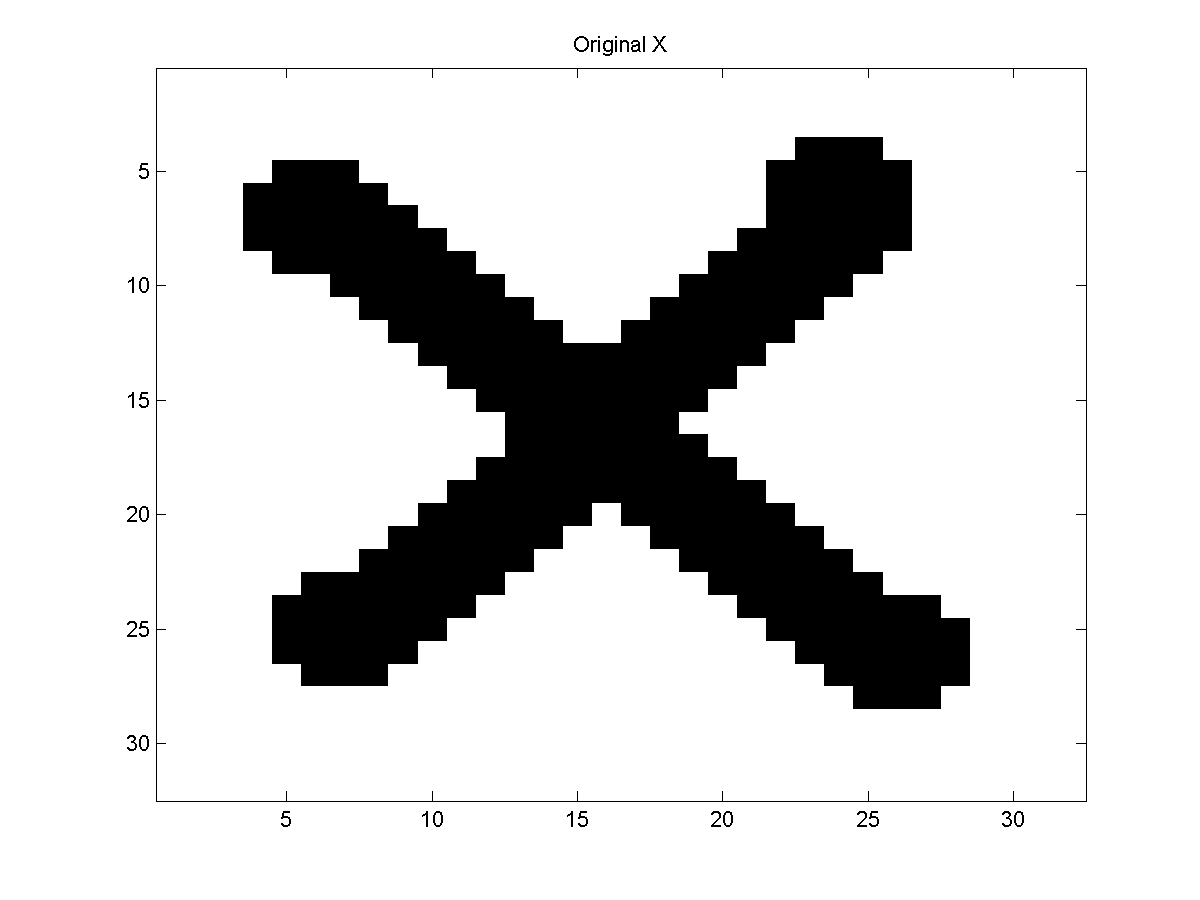
It is a 32 by 32 binary image. If we corrupt it with independent Gaussian noise, it will look something like this:

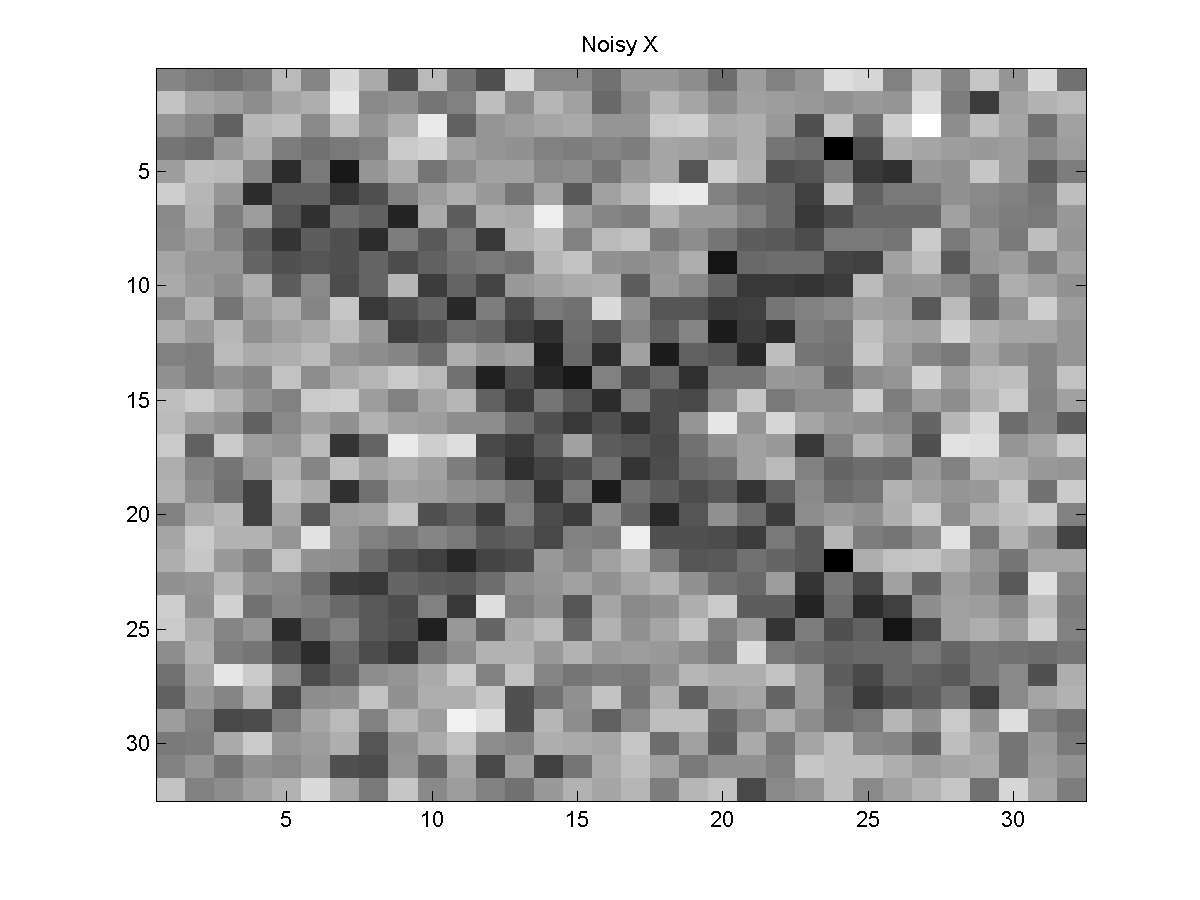
Given the noisy X, our task is to assign binary states to the pixels to try and recover the original X (or whatever other binary image has been corrupted by noise).

The first approach we might try to solve this problem is to threshold the pixel values. Decoding by independently thresholding the pixels gives this result:

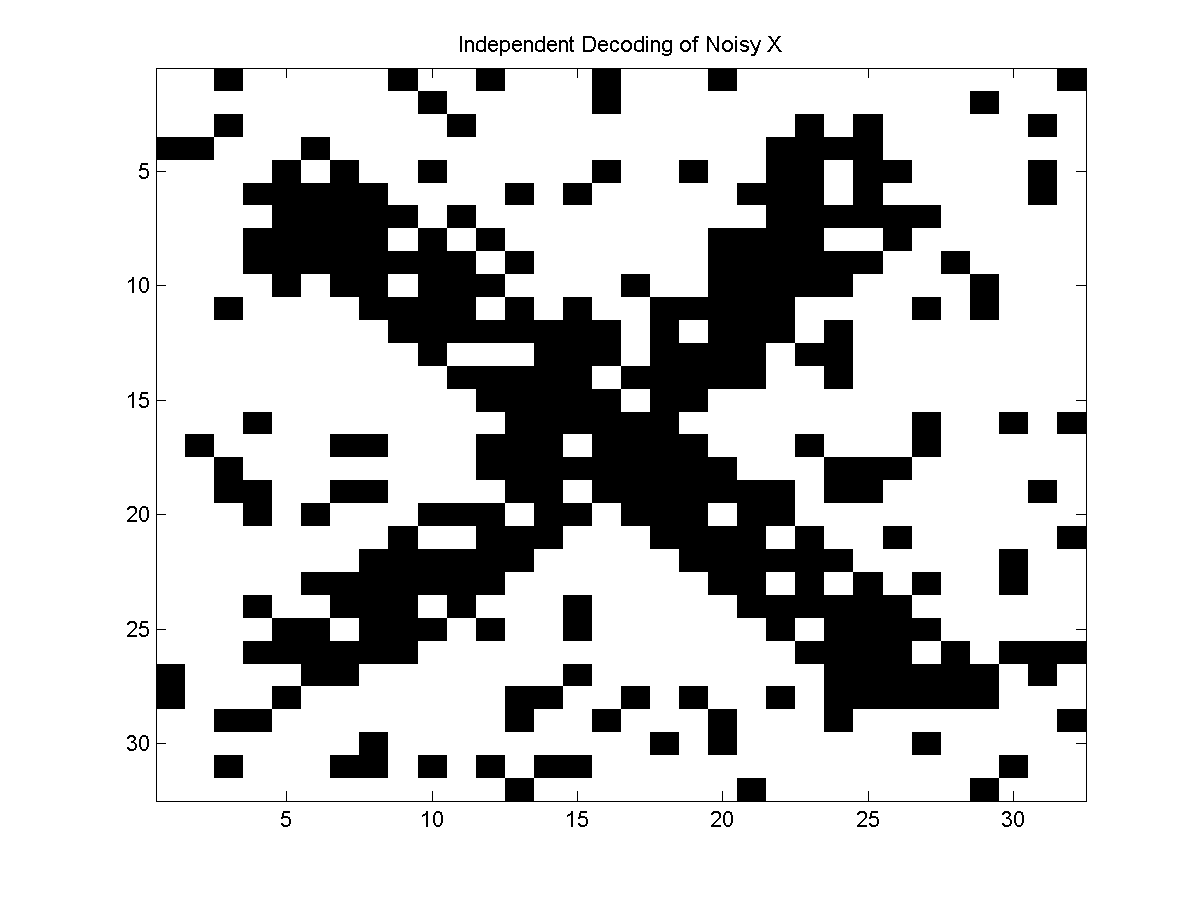
Independently thresholding the pixels doesn't take into account that neighboring pixels are likely to take the same value. One way to model this dependency is with a UGM.

Representing the binary denoising problem with UGM

In our UGM, each node will represent a pixel, and we will place an edge between adjacent pixels. In particular, a pixel will be connected to the pixels above, below, to the left, and to the right. This graph structure forms a 2D lattice, a type of graph structure that has been studied not only for images, but has a long history in statistical physics (e.g. the Ising model). We can make the edgeStruct for a 2D lattice-structured model as follows: 
load X.mat % Load the image
X = X + randn(size(X))/2; % Make a noisy version of it

[nRows,nCols] = size(X);
nNodes = nRows*nCols;
nStates = 2;
 
adj = sparse(nNodes,nNodes);
 
% Add Down Edges
ind = 1:nNodes;
exclude = sub2ind([nRows nCols],repmat(nRows,[1 nCols]),1:nCols); % No Down edge for last row
ind = setdiff(ind,exclude);
adj(sub2ind([nNodes nNodes],ind,ind+1)) = 1;
 
% Add Right Edges
ind = 1:nNodes;
exclude = sub2ind([nRows nCols],1:nRows,repmat(nCols,[1 nRows])); % No right edge for last column
ind = setdiff(ind,exclude);
adj(sub2ind([nNodes nNodes],ind,ind+nRows)) = 1;
 
% Add Up/Left Edges
adj = adj+adj';
edgeStruct = UGM_makeEdgeStruct(adj,nStates);

% Standardize Features
Xstd = UGM_standardizeCols(reshape(X,[1 1 nNodes]),1);
The last line transforms the noisy image intensities so that they have a mean of zero and a standard deviation of 1. We will use the following node potentials: 
nodePot = zeros(nNodes,nStates);
nodePot(:,1) = exp(-1-2.5*Xstd(:));
nodePot(:,2) = 1;
We want to use edge potentials that reflect that neighboring pixels are more likely to have the same label. Further, we expect that they are even more likely to have the same label if the difference in their intensities is small. We incoporate this intuition by using the following Ising-like edge potentials 
edgePot = zeros(nStates,nStates,edgeStruct.nEdges);
for e = 1:edgeStruct.nEdges
   n1 = edgeStruct.edgeEnds(e,1);
   n2 = edgeStruct.edgeEnds(e,2);

   pot_same = exp(1.8 + .3*1/(1+abs(Xstd(n1)-Xstd(n2))));
   edgePot(:,:,e) = [pot_same 1;1 pot_same];
end
In the node and edge potentials, we have used some carefully selected constants, {-1, -2.5, 1.8, .3}. These constants were obtained as a maximum pseudolikelihood estimator, subject to the constraint that the edge potentials are attractive. Having attractive potentials is what will allow us to do efficient decoding in the model.

Approximate Decoding

The 2D lattice structure has 1024 nodes, so brute force decoding is not possible. Further, the loopy structure has a high enough treewidth that it is impractical to use junction trees (the treewidth of a lattice structure is the minimum between the number of rows and the number of columns). We might therefore consider an approximate decoding method. One of the simplest approximate decoding methods (that will be discussed further in the next demo) is the iterated conditional mode (ICM) algorithm. Beginning from some initial assignment of states to nodes, the ICM algorithm cycles through the nodes, greedily maximizing the potential of each node given its neighbors. This continues until no further local improvements are possible. The disadvantage of the ICM method is that it may converge to a local maximum that is not the global maximum. If we take the assignment that maximizes the node potentials to initialize ICM, it converges to the following approximate decoding:

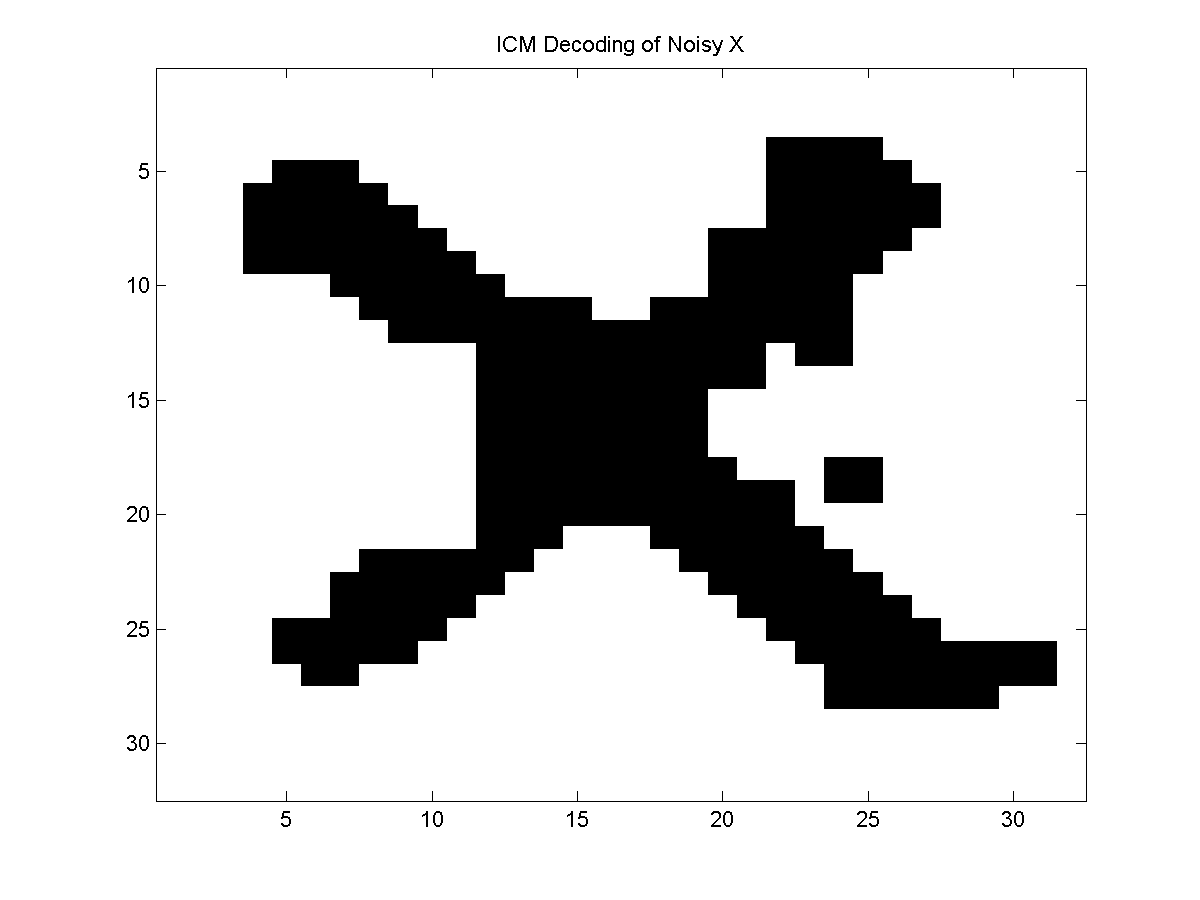
This looks much better than the independent model, but as we will see next the locally optimal decoding found by ICM is not as good as the globally optimal decoding.

Graph Cuts for Optimal Decoding in Binary Sub-Modular UGMs

Somewhat surprisingly, it is possible to find the optimal decoding in this model in polynomial time. This is because the UGM is binary and all its edge potentials satisfy the inequality ep(1,1)*ep(2,2) >= ep(1,2)*ep(2,1), which we refer to as attractive potentials (since they encourage neighboring nodes to take the same state). These two simple restrictions allow us to formulate finding the optimal decoding as a maximum flow problem (that can solved in polynomial-time), where the optimal decoding is given by the minimal graph cut in the flow network. Indeed, we can formulate decoding as a maximum flow problem whenever these two restrictions are satisfied, no matter what graph structure is used.

We can use UGM to find the optimal decoding in a model satisfying these restrictions using: 

optimalDecoding = UGM_Decode_GraphCut(nodePot,edgePot,edgeStruct);
imagesc(reshape(optimalDecoding,nRows,nCols));
colormap gray
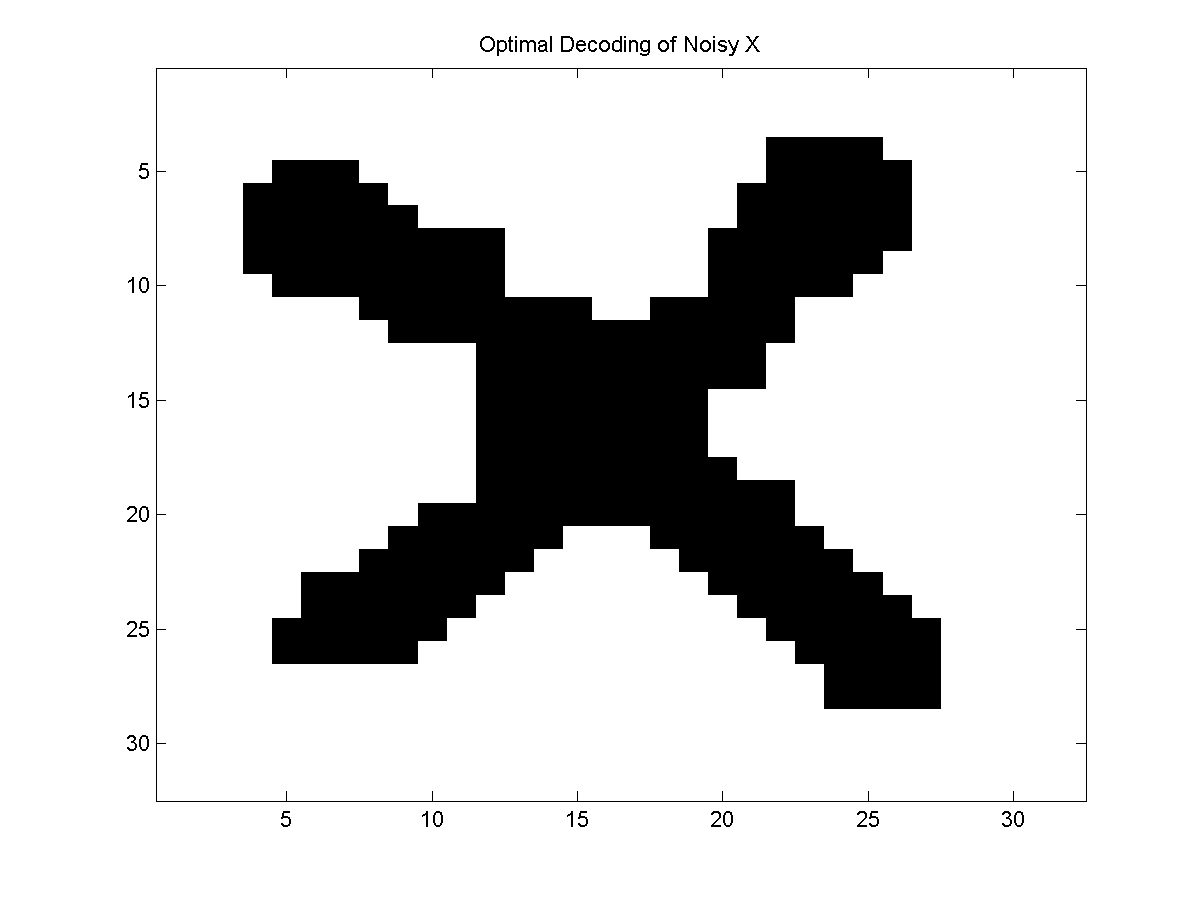
The optimal decoding of the UGM gives the following more satisfactory result:

Notes

As mentioned above, decoding by graph cuts will be substantially faster if the mex wrapper to the maxflow code is found on the path.

Graph cuts were originally proposed for finding the optimal decoding in an image denoising problem in:

The formulation of the decoding problem as a maximum flow problem for binary models under the associative condition is due to: PREVIOUS DEMO NEXT DEMO
Mark Schmidt > Software > UGM > GraphCuts Demo