BDAGL: Bayesian DAG learning

This Matlab/C/Java package (pronounced "be-daggle") supports Bayesian inference about (fully observed) DAG (directed acyclic graph) structures using dynamic programming and MCMC. The code is under the Lesser (formerly Library) GNU Public License. (Click here for why.)
Written by Daniel Eaton and Kevin Murphy, September 2006 -- June 2007.

Quick start

This software has no external dependencies, i.e., all relevant code is included. The code has only been tested on Matlab 7.4 (R2007a) and is not guaranteed to work on earlier versions.

Download and unzip BDAGL.zip.
In Matlab, change the directory to the newly created BDAGL folder.
Run the script mkPath, which adds all necessary folders to the path, and compiles Mex files (if required). The resulting files are called .mexw32 if compiled on Windows under Matlab 7.1 or newer; they are called .dll if compiled on Windows on older Matlabs; they are called .mexglx if compiled on Unix; etc.
Type runDemos. Consult the documentation below for an explanation of what these demos are doing.
See also this simple demo

Major features

The main features of the package are described below. See the references for details (the user is assumed to be familiar with these papers). The main restrictions are that it cannot handle hidden nodes or undirected graphs. In addition, it has only been tested on small problems (20 nodes or fewer); however, it can compute exact answers on such problems (under restrictive assumptions about the prior).

Computes the most probable graph G_map = arg max_G p(G|D) exactly using the dynamic programming (DP) algorithm of Silander & Myllymaki UAI'06, where G is a DAG and D is data. This takes O(d 2^d) time and space, so is limited to about 20 variables. This takes about 5 seconds for d=10 to about 5 minutes for d=20. (For some Java code to do approximate MAP structure learning using simulated annealing or hill climbing, see Banjo. For some Matlab code to do approximate MAP structure learning using local search and L1-based variable selection, see L1DAGlearn.)
Computes exact edge marginals using Bayes model averaging, p(G_{ij}=1|D) = sum_G I(G(i,j)=1) p(G|D), using the DP algorithms of Koivisto & Sood JMLR'04, and Koivisto UAI'06. This takes O(d 2^d) time and space, so is limited to about 20 variables. This takes about 5 seconds for d=10 to about 5 minutes for d=20. See also Koivisto's C++ package REBEL, which implements the same functionality. (Our code seems to be slightly faster, but they should give identical results.)
Computes edge marginals p(G_{ij}=1|D) (or other posterior features) approximately using MCMC in the space of DAGs with various proposal distributions. Options include the standard local proposal (add/ delete/ reverse edge), and a global proposal based on DP (see Eaton & Murphy, UAI'07) These methods handle arbitrary graph priors. It also supports (using restrictive priors) MCMC in the space of total orders (see Friedman & Koller, MLJ'03), and Gibbs sampling on the adjacency matrix. In principle, these algorithms avoid the 2^d bottleneck of exact DP, although the current implementation may not scale much beyond d=20....
Supports various models of intervention (perfect, imperfect, uncertain, soft) for learning causal networks from experimental data; see Eaton & Murphy, AIStats'07 and our (rejected) JMLR'07 submission for details.
Supports BDe score for Multinomial models with Dirichlet priors, and BGe score for Gaussian models with Gaussian-Gamma priors. Could be extended to more flexible CPDs/ priors using BIC.
Supports DBN learning from (fully observed) time series data.
Supports posterior predictive density modeling for test data, integrating over structures and parameters. (Also supports plug-in prediction.)
Efficiently computes the sufficient statistics for discrete CPDs from large data sets using ADtrees (see Moore & Lee, JAIR'98).
Efficiently represents samples of DAGs using Java hash keys.
Includes the discretized protein phosphorylation data from the T-cell signaling network from Sachs et al, Science '05 (distributed with permission of Karen Sachs).

Basic DP

We illustrate the core DP algorithms using the 5 node cancer network below; see cancerDemo for the details.

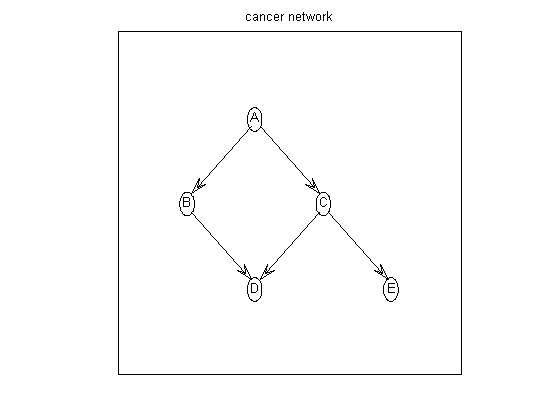
Suppose the graph prior is uniform over all parents sets of size <= maxFanIn. We first construct the all families log prior matrix, defined as

aflp(i,gi) =  log p(parents of i = gi)

which is a 5x32 matrix, since there are 2^5=32 possible parent sets. (Actually, there are only 2^4, since a node cannot include itself; the corresponding illegal entries are set to -Inf.)

nNodes = 5;
maxFanIn = nNodes - 1; 
aflp = mkAllFamilyLogPrior( nNodes, 'maxFanIn', maxFanIn );

Now let us create some data. We can sample data from the cancer network, using random CPTs, using cancerMakeData. The resulting data is stored in cancerDataObs.mat. Let us load this and compute the 5x32 all families log marginal likelihood matrix, defined as

aflml(i,gi) = sum_n log p(X(i,n) | X(gi,n))

We can do this as follows:

load 'cancerDataObs.mat' % from cancerMakeData 
% data is size d*N (nodes * cases), values are {1,2}
aflml = mkAllFamilyLogMargLik( data, 'nodeArity', repmat(2,1,nNodes), ...
			       'impossibleFamilyMask', aflp~=-Inf, ...
			       'priorESS', 1);

This uses ADtrees to cache the sufficient statistics (see Moore98 for details). This is implemented in C.

If we have Gaussian data, we can use the BGe score instead:

aflml = mkAllFamilyLogMargLik( data, 'impossibleFamilyMask', aflp~=-Inf,
  'cpdType', 'gaussian' );

Finally we are ready to compute the optimal DAG

optimalDAG = computeOptimalDag(aflml); % MLE, max p(D|G)
%optimalDAG = computeOptimalDag(aflml+aflp); % MAP, max p(D,G)

We can also compute exact edge marginals using DP:

epDP = computeAllEdgeProb( aflp, aflml );

In this simple setting, we can compute exact edge marginals by brute force enumeration over all 29,281 DAGs of 5 nodes:

epEnumer = computeAllEdgeProb_Exact(0, aflml); % 0 denotes uniform prior

If we visualize these heat maps, we see that they are different. (DP in top left is not the same as enumeration in bottom right.) This is because the DP algorithm implicitly assumes a special "modular" prior; see Friedman03 and Koivisto04. We will fix this below using MCMC sampling.

Basic MCMC

Let us now fix the biased p(G) problem by using Metropolis Hastings, as described in Eaton07_uai. We use a proposal that 10% of the time samples DAGs based on the DP edge marginals, and 90% of the time does standard local moves.

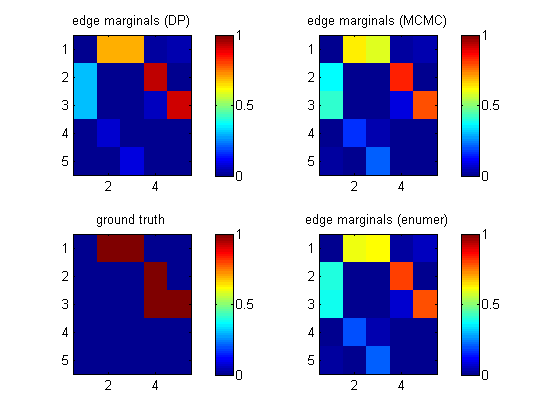
[samples, diagnostics, runningSum] = sampleDags(@uniformGraphLogPrior, aflml, ...
				    'burnin', 100, 'verbose', true, ...
				    'edgeMarginals', epDP, 'globalFrac', 0.1, ...
				    'thinning', 2, 'nSamples', 5000);
epMCMC = samplesToEdgeMarginals(samples);

The heat map above (top right) shows that this gives the same results as exhaustive enumeration with a uniform prior. The MCMC routine uses hash tables to represent samples of graphs compactly.

Order sampling (Friedman03) is in the OrderMcmc directory, but is undocumented. We also support the importance sampling reweighting of Ellis06.

Interventional data

To learn the orientation of all the edges in a DAG, we need interventional data. We will illustrate this using the cancer network; see cancerDemoInter for details.

Let us load some data where we have performed a perfect intervention on node A. The 5x700 matrix clamped is defined so clamped(i,n)=1 iff node i is set by intervention in case n. We modify the computation of the marginal likelihoods to remove cases that were set by intervention.

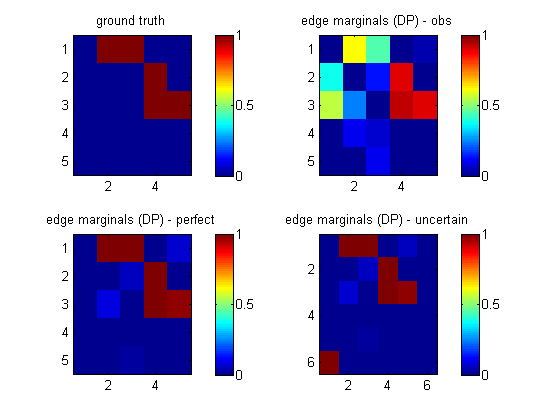
load 'cancerDataInterA.mat' % from cancerMakeData 
nNodes = 5;
maxFanIn = nNodes - 1; 
aflp = mkAllFamilyLogPrior( nNodes, 'maxFanIn', maxFanIn ); 
aflml_perfect = mkAllFamilyLogMargLik( data, 'nodeArity', repmat(2,1,nNodes), ...
			       'impossibleFamilyMask', aflp~=-Inf, ...
			       'priorESS', 1, ...
			       'clampedMask', clamped);
epDP_perfect = computeAllEdgeProb( aflp, aflml_perfect );

This lets us recover the true structure uniquely. If we ignore the fact that this is interventional data (by omitting the clamped parameter), we get the wrong answer, as shown in the top right plot below (labeled 'obs').

Uncertain interventions

If we do not know which nodes are affected by the intervention, we can add the intervention node to the graph and learn its children (targets), as described Eaton & Murphy, AIStats'07 (see our (rejected) JMLR'07 submission for more details).

Let us call the intervention node number 6. This node is always clamped; let us put it in state 1 half the time, and state 2 for the rest, and append this to the normal data.

N = size(data,2);
nObservationCases = N/2; % # observational data cases
nInterventionCases = N/2; % no interventions
assert(N==nObservationCases+nInterventionCases);
data_uncertain = [data; [ones(1,nObservationCases) 2*ones(1,nInterventionCases)]];
clamped_uncertain = [zeros(size(clamped)); ones(1,N)];

When learning the topology, we do not want to allow connections between the intervention nodes, or back from the backbone nodes to the intervention nodes. We can enforce this by putting the intevention node in layer 1, and the other nodes in layer 2, and restricting the fan-in between and within layers as follows

% fan-in
%     L1  L2
% L1   0   1    % only 1 intervention parent allowed for L2 nodes
% L2   0   max  % only max # paretns allowed in total for L2 nodes

maxFanIn_uncertain = [ 0 1 ; 0 maxFanIn ]; 
layering = [2*ones(1,nNodes) 1];
nodeArity = 2*ones(1,nNodes);
nodeArity_uncertain = [nodeArity 2];

aflp_uncertain = mkAllFamilyLogPrior( nNodes+1, 'maxFanIn', maxFanIn_uncertain, ...
				      'nodeLayering', layering );

aflml_uncertain = mkAllFamilyLogMargLik(data_uncertain, ...
		'nodeArity', nodeArity_uncertain, 'clampedMask', clamped_uncertain, ...
		'impossibleFamilyMask', aflp_uncertain~=-Inf, 'verbose', 0 );

epDP_uncertain = computeAllEdgeProb( aflp_uncertain, aflml_uncertain );

We see from the picture above (bototm right, labeled 'uncertain') that we learn that node 6 targets node 1 (A), and we also correctly recover the backbone.

Layering

In general, layering is defined as follows. The maxFanIn matrix is upper triangular. M(i,j) is the maximum fan-in allowed from j into i; M(i,i) is the maximum fan-in from any preceeding layer; use -1 to mean "don't care".

For example, suppose nodes (1,3) are in layer 1 and nodes (2,4,5) are in layer 2. We can allow connections from L1 to L2, and within L2, as follows:

layering = [1 2 1 2 2 ]; 
maxFanIn = [0 -1 ; 0 3 ];

M(1,1)=0 means no connections into L1. M(1,2)=-1 means no constraints on the number of L1->L2 connections (modulo constraints imposed by M(2,2)); M(2,2)=3 means at most 3 parents for any node in L2.

DBNs

We can use the DP algorithm to learn edge marginals for fully observed DBNs. If we have d nodes per time slice, we just learn a 2d x 2d DAG, with a layering constraint that there can be no connections backwards in time. The key function is transformDbnData which takes a dxT time series and computes a (2d)x(T-1) matrix of two-slice samples. Then we use the standard DP code above. dbnDemo contains 2 demos

An HMM topology but with all nodes observed
A biologically motivated DBN, from Husmeier03.

Graph layout

A very simple graph drawing function (based on code by Ali Cemgil) is illustrated in cancerDemo and can be called as shown below:

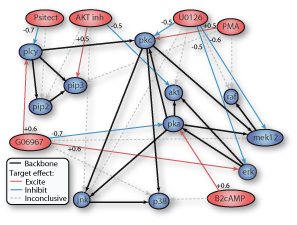
myDrawGraph(dag, 'labels', labels, 'layout', graphicalLayout)

If the layout coordinates are omitted, the function lays the nodes out in a circle.

To achieve higher quality results, I recommend the free windows program called pajek. A function adj2pajek2.m will convert a dag to the pajek format; this file can then be read in and automatically layed out in a pretty way.

Analysing biological data

A more interesting example can be found in sachsDemo, where we learn the MAP optimal DAG and edge marginals using DP from 5400 interventional samples of 11 variables from the Sachs05 paper. The effects of various graph priors, taken from Werhli07, are studied in sachsDemoPriors using MCMC. See also Ott04. (Ott seems to have independently invented Koivisto's DP algorithm, and applied it to biological data, long before we were aware of this.)

References

@inproceedings{Eaton07_jmlr,
  author = "D. Eaton and K. Murphy",
 title = {{Belief net structure learning  from uncertain interventions}},
 journal = jmlr,
 note= "Submitted",
 year = 2007,
 url = "http://www.cs.ubc.ca/~murphyk/Papers/jmlr07.pdf"
}

@inproceedings{Eaton07_aistats,
  author = "D. Eaton and K. Murphy",
 title = {{Exact Bayesian structure learning from uncertain interventions}},
 booktitle = "AI/Statistics",
 year = 2007
 url = "http://www.cs.ubc.ca/~murphyk/Papers/aistats07.pdf"
}

@inproceedings{Eaton07_uai,
  author = "D. Eaton and K. Murphy",
 title = {{Bayesian structure learning using dynamic programming and MCMC}},
 booktitle = uai,
 year = 2007,
 url = "http://www.cs.ubc.ca/~murphyk/Papers/eaton-uai07.pdf"
}

@inproceedings{Ellis06,
 title = {{Sampling Bayesian Networks quickly}},
 author = "B. Ellis and W. Wong",
 booktitle = "Interface",
 year = 2006
}

@article{Friedman03,
 title = {{Being Bayesian about Network Structure: A Bayesian Approach to Structure Discovery in Bayesian Networks}},
 author = "N. Friedman and D. Koller",
  journal = "Machine Learning",
 volume = 50,
  pages = "95-126",
 year = 2003
}

@article{Husmeier03,
 author = "D. Husmeier",
 title = {{Sensitivity and specificity of inferring genetic regulatory
interactions from microarray experiments with dynamic Bayesian networks}},
 journal = "Bioinformatics",
 volume = 19,
 pages = "2271--2282",
 year = 2003
}

@article{Koivisto04,
 author = "M. Koivisto and K. Sood",
 title = {{Exact Bayesian structure discovery in Bayesian networks}},
 journal = jmlr,
 year = 2004,
 volume = 5,
 pages = "549--573",
url = {{http://www.ai.mit.edu/projects/jmlr//papers/volume5/koivisto04a/koivisto04a.pdf}}}

@inproceedings{Koivisto06,
 author = "M. Koivisto",
 title = {{Advances in exact Bayesian structure discovery in Bayesian networks}},
 booktitle = uai,
 year = 2006,
 url = {http://www.cs.helsinki.fi/u/mkhkoivi/publications/uai-2006.pdf}
}

@article{Moore98,
    author = "A.  Moore and M. Lee",
    title = "Cached Sufficient Statistics for Efficient Machine Learning with Large Datasets",
    journal = jair,
    volume = "8",
    pages = "67-91",
    year = "1998"
   url = "citeseer.nj.nec.com/moore97cached.html"
}


@inproceedings{Ott04,
 title = "Finding optimal models for small gene networks",
 author = "Sascha Ott and Seiya Imoto and Satoru Miyano",
 booktitle= "Pacific Symposium on Biocomputing",
 year = 2004
 url = "http://helix-web.stanford.edu/psb04/ott.pdf"
}


@article{Sachs05,
 title = "Causal Protein-Signaling Networks Derived from Multiparameter Single-Cell Data",
 author = "K. Sachs and O. Perez and D. Pe'er and D. Lauffenburger and G. Nolan",
 journal = "Science",
 year = 2005,
  volume = 308,
 page = "523"
}

@inproceedings{Silander06,
 author = "T. Silander and P. Myllymaki",
  title = {{A simple approach for finding the globally optimal Bayesian network structure}},
  year = 2006,
  booktitle = uai,
  url = {{http://eprints.pascal-network.org/archive/00002135/01/main.pdf}}
}

@article{Werhli07,
 author = "A. Werhli and D. Husmeier",
 title = "Reconstructing Gene Regulatory Networks with Bayesian
Networks by Combining Expression Data with Multiple Sources of Prior Knowledge",
 journal = "Statistical Applications in Genetics and Molecular Biology",
 year = 2007,
 volume = 6,
 number = 1
}