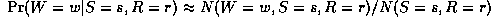
One needs to specify two things to describe a BN: the graph topology (structure) and the parameters of each CPD. It is possible to learn both of these from data. The basic idea is to use maximum likelihood (ML) to find the parameters, and penalized ML to find the best structure (to avoid overfitting) (see Heckerman, 1996 and Krause, 1998). The penalty can be expressed as a prior, which says simpler models are more likely, or in terms of the Minimum Description Length principle.
If the value of every node is observed (the complete data case), finding the ML parameters amounts to counting, e.g.,
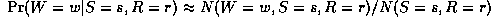
where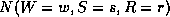 
is the number of times this event occurs in the
training set. (In the case of Gaussian distributions, the sufficient
statistics are the sample mean and variance.)
We can find the best structure by local search through
model space.
If we have missing information, we need to perform inference to compute the expected sufficient statistics. We can then use EM to find the ML parameters, and SEM to find the best topology (see Friedman, 1997).
The key advantage of BNs is that they have a small number of
parameters, and hence require less data to learn.
For example,
we can specify the joint distribution over n nodes using only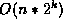 
parameters (where 
is the maximum fan-in
of any node), instead of the 
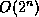which would be required for an
explicit representation.