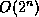Once we have the complete
joint probability distribution (JPD), we can answer all possible inference
queries by marginalization (summing out over irrelevant variables), as
illustrated above. However, the JPD has size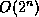 
, where 
is the
number of nodes, and we have assumed each node can have 2
states. Hence summing over the JPD takes exponential time.
However, we can exploit the factored nature of the JPD to compute marginals more efficiently. The key idea is "push sums in" as far as possible when summing (marginalizing) out irrelevant terms, e.g.,
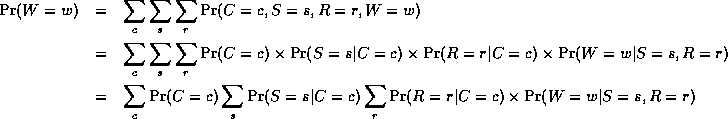
Notice that, as we perform the innermost sums, we create new terms, which need to be summed over in turn e.g.,
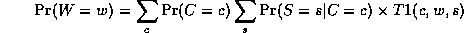
where
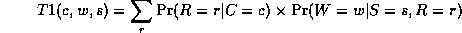
Continuing in this way,
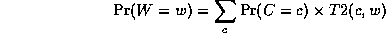
where
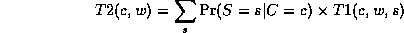
A convenient way to handle the book-keeping arising from all these intermediate terms is by using the bucket elimination algorithm.
The amount of work we perform when computing a marginal is bounded by the size of the largest term that we encounter. Choosing a summation (elimination) ordering to minimize this is NP-hard, although greedy algorithms work well in practice (see Kjaerulff, 1990).
If we wish to compute several marginals at the same time, we can use Dynamic Programming to avoid repeated computation. If the underlying undirected graph of the BN is acyclic (i.e. a tree), we can use a local message passing algorithm due to Pearl (see Peot and Shachter, 1991). In the case of DBNs with the structure shown above (which is acyclic), Pearl's algorithm is equivalent to the forwards-backwards algorithm for HMMs, or to the Kalman-RTS smoother for LDSs (see Ghahramani, 1997).
If the BN has undirected cycles (as in the sprinkler example), we need to first create an auxiliary data-structure, called a join tree, and then apply the DP algorithm to the join tree (see Jensen, 1996 and Shafer and Lauritzen, 1996). The nodes of a join tree are subsets of nodes of the original BN, and satisfy the following property: if x is a member of join tree nodes i and j, then x must be a member of every node on the path between i and j. This property ensures that local propogation of information leads to global consistency.
We can create the join tree by moralizing and
triangulating the BN graph (see Kjaerulff, 1990), and then finding the maximum
cliques. Triangulation ensures that there are no chordless cycles of
length greater than 4. Intuitively, triangulation connects together
those nodes that
feature in a common term when summing out; in the example above,
we connect C to W and get the clique CWS, corresponding to the
intermediate te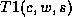rm 
. The process of moralization connects
togther unmarried parents who share a common child: this ensures there
will be a clique that contains terms of the form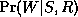 
.