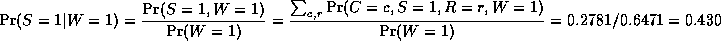
The most common task we wish to solve using Bayesian networks is probabilistic inference. For example, suppose we observe the fact that the grass is wet. There are two possible causes for this: either it is raining, or the sprinkler is on. Which is more likely? We can use Bayes' rule to compute the posterior probability of each explanation (using 1 to represent true and 0 to represent false).
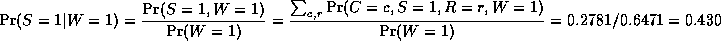
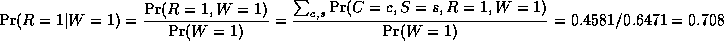
where
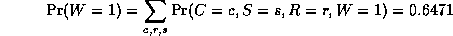
is a normalizing constant, equal to the probability (likelihood) of the data.
So we see that it is more likely that the grass is wet because it is raining: the likelihood ratio is 0.4581/0.2781 = 1.447. Notice that the two causes "compete" to "explain" the observed data. Hence S and R become conditionally dependent given that their common child, W, is observed, even though they are marginally independent.
In the above example, we had evidence of an effect (wet grass), and inferred the most likely cause. This is called diagnostic reasoning: from effects to causes ("bottom up"), and is a common task in expert systems. Bayes nets can also be used for causal "top down" reasoning. For example, we can compute the probability that the grass will be wet given that it is cloudy. In this case, we must be careful not to double-count evidence: the information from S and R flowing into W is not independent, because it came from a common cause, C.
In a DBN, the goal is to compute the probability of the hidden state
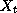 given all the evidence so far, i.e.,
given all the evidence so far, i.e.,
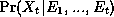 (filtering), or (in off-line mode) given
<i>all</i> the evidence
i.e.,
(filtering), or (in off-line mode) given
<i>all</i> the evidence
i.e., 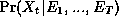 for
for 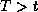 (smoothing). We might also be interested
in predicting the future,
(smoothing). We might also be interested
in predicting the future, 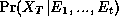 .
.