Dynamic Bayesian Networks (DBNs)



Next: Inference
Up: Representation
Previous: Representation
When the random variables change over time (a stochastic
process), we use a Dynamic Bayesian Network (DBN).
Kalman filter models and Hidden Markov Models (HMMs) are special cases
of DBNs in which we assume there is a <i>single</i> (possibly
vector-valued) state variable.
When there are many loosely-coupled discrete state variables,
DBNs are a more efficient way of representing the system.
If, however, there is a single variable, which undergoes a sequence of
state transitions (as in a stochastic automaton),
HMMs are a better choice.
A generic DBN model has two components:
The state evolution model describes
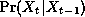 , and the
observation model describes
, and the
observation model describes
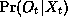 . In the case of a Kalman
filter model, we
assume the state evolution model and observation models are linear
functions subject to Gaussian noise. In the case of an HMM, the system
can have arbitrary, non-linear dynamics, although the number of parameters
is exponential in the size of the state space,
. In the case of a Kalman
filter model, we
assume the state evolution model and observation models are linear
functions subject to Gaussian noise. In the case of an HMM, the system
can have arbitrary, non-linear dynamics, although the number of parameters
is exponential in the size of the state space, 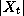 . A DBN provides a means
to represent the transition and observation functions in a compact
form (i.e., using fewer parameters). This can make inference and
learning more efficient (less time and less data, respectively).
. A DBN provides a means
to represent the transition and observation functions in a compact
form (i.e., using fewer parameters). This can make inference and
learning more efficient (less time and less data, respectively).
Sun Oct 18 12:11:28 PDT 1998
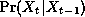 , and the
observation model describes
, and the
observation model describes
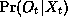 . In the case of a Kalman
filter model, we
assume the state evolution model and observation models are linear
functions subject to Gaussian noise. In the case of an HMM, the system
can have arbitrary, non-linear dynamics, although the number of parameters
is exponential in the size of the state space,
. In the case of a Kalman
filter model, we
assume the state evolution model and observation models are linear
functions subject to Gaussian noise. In the case of an HMM, the system
can have arbitrary, non-linear dynamics, although the number of parameters
is exponential in the size of the state space, 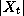 . A DBN provides a means
to represent the transition and observation functions in a compact
form (i.e., using fewer parameters). This can make inference and
learning more efficient (less time and less data, respectively).
. A DBN provides a means
to represent the transition and observation functions in a compact
form (i.e., using fewer parameters). This can make inference and
learning more efficient (less time and less data, respectively).