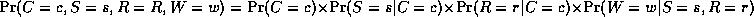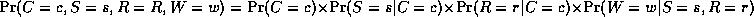
Bayesian Networks (also called probabilistic networks or belief networks) are a graphical way of representing (in)dependence relationships. Nodes in the graph represent random variables, and we draw an arc from A to B if A "directly influences" B (we will give the formal semantics later). Here is a simple example.
In this picture (from Russell and Norvig, 1995), we see that the event "grass is wet" (W=true) has two possible causes: either the water sprinker is on (S=true) or it is raining (R=true). The probability that the W node is true depends on the state of W's parents. This conditional probability distribution (CPD) can be specified in tabular form as shown in the picture. For example, we see that Pr(W=true | S=true, R=false) = 0.9 (and hence, Pr(W=false | S=true, R=false) = 1 - 0.9 = 0.1). Since the C node has no parents, its CPD specifies the prior probability that it is cloudy.
The formal independence assumption encoded in the graph is that a node is conditionally independent of all its non-descendants given its parents: this is called the directed Markov property (see Pearl, 1988). This means that if we topologically order the nodes, we can represent the joint probability distribution (JPD) as a product of local factors using the chain rule. For example, referring to sprinkler network,