| | | Parent Contexts and Contextual Belief Networks |
As in the definition of a belief network, let's assume that we have a total ordering of the variables, X1,...,Xn.
Definition. Given variable Xi, we say that C=c, where C subset {Xi-1...X1} and c in dom(C), is a parent context for Xi if Xi is contextually independent of the predecessors of Xi (namely {Xi-1...X1}) given C=c.
Example.
Consider the belief network and conditional probability table of Figure
*. The predecessors
of variable E are A,B,C,D,Y,Z. A set of minimal parent
contexts for E is { {a,b}, {a, We can often (but not always) represent contextual independence in
terms of trees.
The left side of Figure * gives a tree-based
representation for the conditional probability of E given its
parents. In this tree, internal nodes are labelled with parents of E
in the belief network. The left child of a node corresponds to
the variable labelling the node being true, and the right child
to the variable being false. The leaves are labelled with the
probability that E is true. For example P(e|a&~b}, {~a,c},
{~a,~c,d,b}, {~a,~c,d,~b}, {~a,~c,~d}}. This is a mutually exclusive and exhaustive set of parent contexts. The probability of E given values for its
predecessors can be reduced to the probability of E given a parent
context. For example:
In the belief network, the parents of E are A,B,C,D. To specify
the conditional probability of E given its parents, the traditional
tabular representation (as in Figure *) require 24 = 16
numbers instead of the 6 needed if we were to use the parent contexts
above. Adding an extra variable as a parent to E doubles the size of
the tabular representation, but if it is only relevant in a single
context it may only increase the number of parent contexts
by one.
P(e|a,b,c, ~d,y,~z) = P(e|a,b)
P(e| ~a,b,c,~d,y,~z) = P(e|~a,c)
P(e| ~a,~b,c, d,~y,~z) = P(e|~a,c).
Tree-structured
representations of the conditional probabilities for E, B,
and D given
their parents. Left branches correspond to true and right branches to
false. Thus, for example, P(e|a &b) = 0.55, P(e|a &
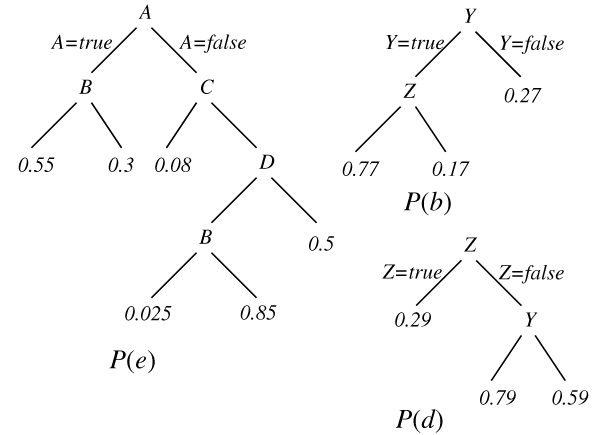
~b) = 0.3, P(e|~a &~c &d &b) = 0.025 etc.~b) = 0.3,
irrespectively of the value for C or D. In the tree-based
representation the variable (E in this case) is contextually
independent of its predecessors given the context defined by a path
through the tree. The paths through the tree correspond to parent
contexts.
Before showing how the structure of parent contexts can be exploited in inference, there are a few properties to note:
~c, ~b}. b &~c is not minimal as ~c is also a
parent context. Another mutually exclusive and exhaustive set of
parent contexts for this example is {b&c, ~b &c, ~c}. The set of minimal parent contexts, {b&c, ~b , ~c}, isn't a mutually exclusive and exhaustive set as the elements
are not pairwise incompatible.
One could imagine using arbitrary Boolean formulae in the contexts. This was not done as it would entail using theorem proving (or a more sophisticated subsumption algorithm) during inference. We doubt that this would be worth the extra overhead for the limited savings.
~a,c}, {~b,~c}, {a,~b,c}, {~a,b,~c}}
doesn't directly translate into a decision tree. More importantly, the
operations we perform don't necessarily preserve the tree structure.
Section * shows how we can do much better than an
analogous tree-based formulation of our inference algorithm.
Definition. A contextual belief network is an acyclic directed graph where the nodes are random variables. Associated with each node Xi is a mutually exclusive and exhaustive set of parent contexts, Pii, and, for each pi in Pii, a probability distribution P(Xi|pi) on Xi. Thus a contextual belief network is like a belief network, but we only specify the probabilities for the parent contexts.
For each variable Xi and for each assignment Xi-1=vi-1,..., X1=v1 of values to its preceding variables, there is a compatible parent context piXivi-1...v1. The probability of a complete context (an assignment of a value to each variable) is given by:
This looks like the definition of a belief network (equation (*)), but which variables act as the parents depends on the values. The numbers required are the probability of each variable for each element of the mutually exclusive and exhaustive set of parent contexts. There can be many fewer of these than the number of assignments to parents in a belief network. At one extreme, there are the same number; at the other extreme there can be exponentially many more assignments of values to parents than the number of elements of a mutually exclusive and exhaustive set of parent contexts.
P(X1=v1,...,Xn=vn) = PRODi = 1n P(Xi=vn|Xi-1=vi-1,..., X1=v1) = PRODi = 1n P(Xi=vi|piXivi-1...v1)
| | | Parent Contexts and Contextual Belief Networks |