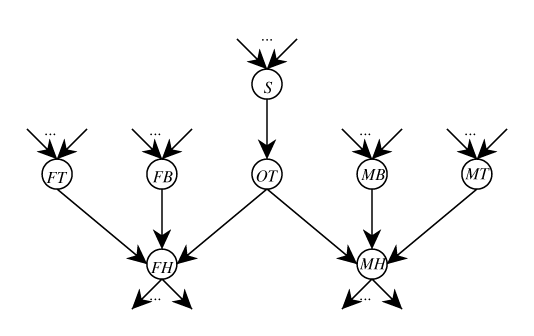
Figure * shows a fragment of a belief network.
A fragment of a belief network: OT to eliminate.
This is an elaboration
of Example *, where what affects the inside temperature
depends on whether the air conditioning is broken or is working. All the variables
are Boolean. We use the following interpretation:
- FB
- Fred's air conditioning is broken
- FT
- Fred's thermostat setting is high
- OT
- Outside temperature is hot
- FH
- Fred's house is hot
- MB
- Mary's air conditioning is broken
- MT
- Mary's thermostat setting is high
- MH
- Mary's house is hot
- S
- Season, that is true if it is Summer
The
ancestors of FT, FB, S, MB, and MT are not shown. They can be
multiply connected. Similarly, the descendants of FH and MH are not
shown. They can be multiply connected.
The outside temperature (OT) is only relevant to Fred's house being
hot (FH) when Fred's air conditioner is broken (FB is true) in
which case Fred's thermostat setting (FT) is not
relevant.
Fred's thermostat setting (FT) is only relevant to Fred's house being
hot (FH) when Fred's air conditioner is working (FB is false),
in which case the outside (OT) is
not relevant. And similarly for Mary's house. See Figure
*. What is important to note is that FH and
MH are dependent, but only if both air conditioners are broken, in
which case the thermostat settings are irrelevant.
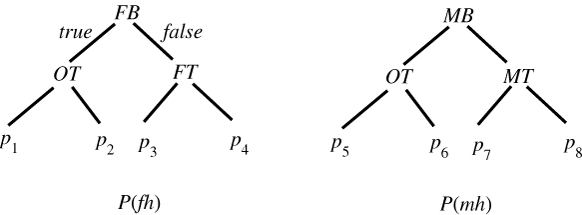
Tree-structured conditional probability tables for A
and for B. Left branches correspond to true and right
branches to false.
Thus p1 = P(a|d &e), p2 = P(a|d &~e), etc.
Suppose we were to sum out OT in VE. Once OT is eliminated, FH and MH
become dependent. In VE and bucket elimination we form a factor
f(FH,MH,FT,FB,MB,MT,S) containing all the remaining variables. This factor
represents P(FH,MH|FT,FB,MB,MT,S) (unless there is a pathological case
such as if MT or MB is a descendent of FH, or if FT or FB is a
descendent of MH). One could imagine a version of VE
that builds a tree-based representation for this factor. We show here
how the confactor-based version is exploiting more structure than this.
If we are to take the contextual independence into account, we need to
consider the dependence between FH and MH when both FB and MB are
true (in which case FT and MT are irrelevant). For all of the other
contexts, we can treat FH and MH as independent. The algorithm CVE
does this automatically.
The conditional probabilities of Figures * and * can be
represented as the following confactors:
fb,|
FH | OT | Value |
|
true | true | p1 |
|
true | false | p2 |
|
false | true | 1-p1 |
|
false | false | 1-p2 |
|
|
|
~fb,|
FH | FT | Value |
|
true | true | p3 |
|
true | false | p4 |
|
false | true | 1-p3 |
|
false | false | 1-p4 |
|
|
|
mb,|
MH | OT | Value |
|
true | true | p5 |
|
true | false | p6 |
|
false | true | 1-p5 |
|
false | false | 1-p6 |
|
|
|
~mb,|
MH | MT | Value |
|
true | true | p7 |
|
true | false | p8 |
|
false | true | 1-p7 |
|
false | false | 1-p8 |
|
|
|
|
OT | S | Value |
|
true | true | p9 |
|
true | false | p10 |
|
false | true | 1-p9 |
|
false | false | 1-p10 |
|
|
|
Eliminating OT from these confactors results in six confactors:
fb&mb,|
FH | MH | S | Value |
|
true | true | true | p9*(p5*p1)+(1-p9)*(p6*p2) |
|
true | true | false | p10*(p5*p1)+(1-p10)*(p6*p2) |
|
true | mbalse | true | p9*((1-p5)*p1)+(1-p9)*((1-p6)*p2) |
|
true | mbalse | false | p10*((1-p5)*p1)+(1-p10)*((1-p6)*p2) |
|
false | true | true | p9*(p5*(1-p1))+(1-p9)*(p6*(1-p2)) |
|
false | true | false | p10*(p5*(1-p1))+(1-p10)*(p6*(1-p2)) |
|
false | false | true | p9*((1-p5)*(1-p1))+(1-p9)*((1-p6)*(1-p2)) |
|
false | false | false | p10*((1-p5)*(1-p1))+(1-p10)*((1-p6)*(1-p2)) |
|
|
|
fb&~mb,|
FH | S | Value |
|
true | true | p9*p1+(1-p9)*p2 |
|
true | false | p10*p1+(1-p10)*p2 |
|
false | true | p9*(1-p1)+(1-p9)*(1-p2) |
|
false | false | p10*(1-p1)+(1-p10)*(1-p2) |
|
|
|
~fb,|
FH | FT | Value |
|
true | true | p3 |
|
true | false | p4 |
|
false | true | 1-p3 |
|
false | false | 1-p4 |
|
|
|
~fb&mb,|
MH | S | Value |
|
true | true | p9*p5+(1-p9)*p6 |
|
true | false | p10*p5+(1-p10)*p6 |
|
false | true | p9*(1-p5)+(1-p9)*(1-p6) |
|
false | false | p10*(1-p5)+(1-p10)*(1-p6) |
|
|
|
~fb&~mb,|
S | Value |
|
true | p9+(1-p9) |
|
false | p10+(1-p10) |
|
|
|
~mb,|
MH | MT | Value |
|
true | true | p7 |
|
true | false | p8 |
|
false | true | 1-p7 |
|
false | false | 1-p8 |
|
|
|
Note that the third and the sixth confactors were there originally and were
not affected by eliminating OT.
The resultant confactors encode the probabilities of {FH,MH} in
the context fb&mb. For all other contexts, CVE considers FH
and MH separately.
The total table size of the confactors after OT is eliminated is
24.
Unlike VE or BEBA, we need the combined effect on FH and MH only for
the contexts where OT is relevant to both FH and MH. For all other
contexts, we don't need to combine the confactors for FH and MH. This is
important, as combining the confactors is the primary source of
combinatorial explosion. By avoiding combining confactors, we can have a
potentially huge saving when the variable to be summed out appears in
few contexts.