Belief Network InferenceBackgroundBelief Networks

Belief Networks

We treat random variables as primitive. We use upper case letters to denote random variables. The domain of a random variable X, written dom(X), is a set of values. If X is a random variable and v in dom(X), we write X=v to mean the proposition that X has value v. The function dom can be extended to tuples of variables. We write tuples of variables in upper-case bold font. If X is a tuple of variables, <X1,...,Xk>, then dom(X) is the cross product of the domains of the variables. We write <X1,...,Xk>=<v1,...,vk> as X1=v1&...&Xk=vk. This is called an instantiation of X. For this paper we assume there is a finite number of random variables, and that each domain is finite.

We start with a total ordering X1,...,Xn of the random variables.

Definition. The parents of random variable Xi, written piXi, are a minimal1 set of the predecessors of Xi in the total ordering such that the other predecessors of Xi are independent of Xi given piXi. That is piXi subset {X1,...,Xi-1} such that P(Xi|Xi-1...X1) = P(Xi|piXi).

A belief network [22] is an acyclic directed graph, where the nodes are random variables2. We use the terms node and random variable interchangeably. There is an arc from each element of piXi into Xi. Associated with the belief network is a set of probabilities of the form P(X|piX), the conditional probability of each variable given its parents (this includes the prior probabilities of those variables with no parents).

By the chain rule for conjunctions and the independence assumption:

P(X1,...,Xn) = PRODi = 1n P(Xi|Xi-1...X1)
= PRODi = 1n P(Xi|piXi)  
This factorization of the joint probability distribution is often given as the formal definition of a belief network.

A B C D P(e|ABCD)
a b c d 0.55
a b c ~d 0.55
a b ~c d 0.55
a b ~c ~d 0.55
a ~b c d 0.3
a ~b c ~d 0.3
a ~b ~c d 0.3
a ~b ~c ~d 0.3
~a b c d 0.08
~a b c ~d 0.08
~a b ~c d 0.025
~a b ~c ~d 0.5
~a ~b c d 0.08
~a ~b c ~d 0.08
~a ~b ~c d 0.85
~a ~b ~c ~d 0.5

A simple belief network and a conditional probability table for E.
 

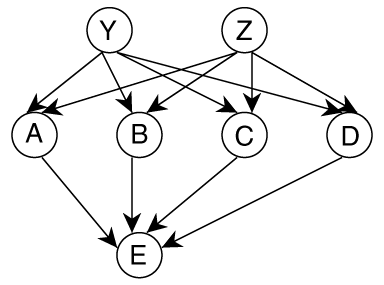
Example. Consider the belief network of Figure *. This represents a factorization of the joint probability distribution:

P(A,B,C,D,E,Y,Z)
= P(E|ABCD) P(A|YZ) P(B|YZ)P(C|YZ) P(D|YZ) P(Y) P(Z)
If the variables are binary3, the first term, P(E|ABCD), requires the probability of E for all 16 cases of assignments of values to A,B,C,D. One such table is given in Figure *.

David Poole and Nevin Lianwen Zhang,Exploiting Contextual Independence In Probabilistic Inference, Journal of Artificial Intelligence Research, 18, 2003, 263-313.

Belief Network InferenceBackgroundBelief Networks