


Next: References
Up: Exploiting Causal Independence in
Previous: Acknowledgements
Theorem
3
Suppose a list of homogeneous factors 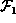 and
a list of heterogeneous factors
and
a list of heterogeneous factors 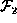 constitute a tidy
factorization of
constitute a tidy
factorization of 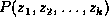 .
If
.
If 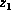 is either a convergent variable, or an old regular variable,
or a new regular variable whose deputy is not in the
list
is either a convergent variable, or an old regular variable,
or a new regular variable whose deputy is not in the
list 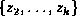 ,
then the procedure
,
then the procedure sum-out1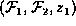 returns
a tidy heterogeneous factorization
of
returns
a tidy heterogeneous factorization
of 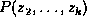 .
.
Proof:
Suppose 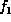 , ...,
, ..., 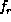 are all the heterogeneous
factors and
are all the heterogeneous
factors and 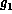 , ...,
, ..., 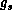 are all the homogeneous factors.
Also suppose
are all the homogeneous factors.
Also suppose 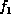 , ...,
, ..., 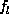 ,
, 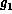 , ...,
, ..., 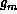 are all the
factors that contain
are all the
factors that contain 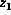 . Then
. Then
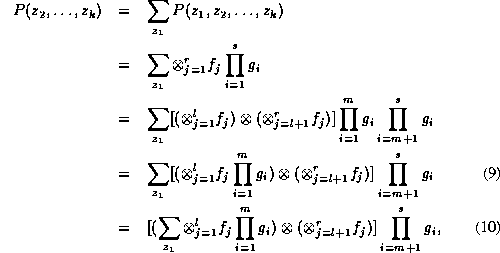
where equation (10) is due to
Proposition 3. Equation (9) is follows from Proposition
4. As a matter of fact,
if 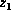 is a convergent variable, then it is the only convergent
variable in
is a convergent variable, then it is the only convergent
variable in 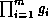 due to the first condition of
tidiness. The condition of Proposition 4 is satisfied because
due to the first condition of
tidiness. The condition of Proposition 4 is satisfied because
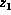 does not appear in
does not appear in 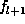 , ...,
, ..., 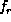 .
On the other hand, if
.
On the other hand, if 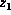 is an old regular variable or a
new regular variable
whose deputy does not appear in
the list
is an old regular variable or a
new regular variable
whose deputy does not appear in
the list 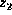 , ...,
, ..., 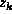 ,
then
,
then
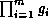 contains no convergent variables due to the second
condition of tidiness. Again the condition of Proposition 4 is satisfied.
We have thus proved that
contains no convergent variables due to the second
condition of tidiness. Again the condition of Proposition 4 is satisfied.
We have thus proved that sum-out1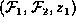 yields a
flexible heterogeneous factorization of
yields a
flexible heterogeneous factorization of 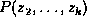 .
.
Let 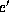 be a convergent variable in the list
be a convergent variable in the list 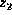 , ...,
, ..., 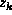 .
Then
.
Then 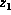 cannot be the corresponding new regular variable e.
Hence the factor
cannot be the corresponding new regular variable e.
Hence the factor 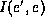 is not touched by
is not touched by
sum-out1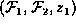 .
Consequently, if we can show that the new factor created
by
.
Consequently, if we can show that the new factor created
by sum-out1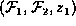 is either
a heterogeneous factor or a homogeneous factor that contain
no convergent variable, then the factorization
returned is tidy.
is either
a heterogeneous factor or a homogeneous factor that contain
no convergent variable, then the factorization
returned is tidy.
Suppose
sum-out1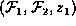 does not create a new homogeneous factor. Then no heterogeneous
factors in
does not create a new homogeneous factor. Then no heterogeneous
factors in 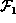 contain
contain 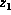 . If
. If 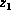 is a convergent variable, say
is a convergent variable, say 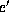 ,
then
,
then 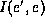 is the only homogeneous factor that
contain
is the only homogeneous factor that
contain 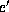 . The new factor is
. The new factor is 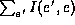 , which does
contain any convergent variables. If
, which does
contain any convergent variables. If 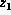 is an old regular variable
or a new regular variable whose deputy is not in the list
is an old regular variable
or a new regular variable whose deputy is not in the list
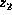 , ...,
, ..., 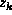 ,
all the factors that contain
,
all the factors that contain 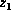 do not contain any convergent variables.
Hence the new factor again does not contain any convergent variables.
The theorem is thus proved.
do not contain any convergent variables.
Hence the new factor again does not contain any convergent variables.
The theorem is thus proved. 



Next: References
Up: Exploiting Causal Independence in
Previous: Acknowledgements
David Poole
Fri Dec 6 15:09:32 PST 1996
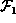 and
a list of heterogeneous factors
and
a list of heterogeneous factors 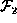 constitute a tidy
factorization of
constitute a tidy
factorization of 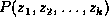 .
If
.
If 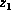 is either a convergent variable, or an old regular variable,
or a new regular variable whose deputy is not in the
list
is either a convergent variable, or an old regular variable,
or a new regular variable whose deputy is not in the
list 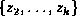 ,
then the procedure
,
then the procedure 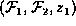 returns
a tidy heterogeneous factorization
of
returns
a tidy heterogeneous factorization
of 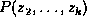 .
.
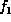 , ...,
, ..., 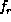 are all the heterogeneous
factors and
are all the heterogeneous
factors and 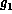 , ...,
, ..., 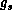 are all the homogeneous factors.
Also suppose
are all the homogeneous factors.
Also suppose 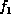 , ...,
, ..., 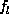 ,
, 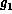 , ...,
, ..., 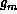 are all the
factors that contain
are all the
factors that contain 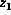 . Then
. Then
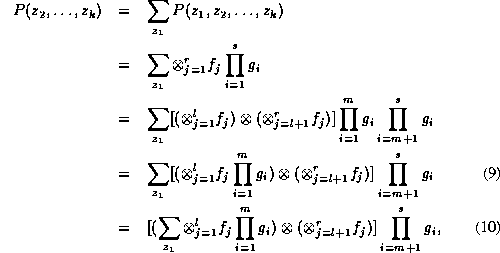
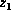 is a convergent variable, then it is the only convergent
variable in
is a convergent variable, then it is the only convergent
variable in 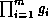 due to the first condition of
tidiness. The condition of Proposition
due to the first condition of
tidiness. The condition of Proposition 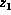 does not appear in
does not appear in 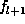 , ...,
, ..., 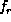 .
On the other hand, if
.
On the other hand, if 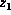 is an old regular variable or a
new regular variable
whose deputy does not appear in
the list
is an old regular variable or a
new regular variable
whose deputy does not appear in
the list 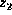 , ...,
, ..., 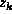 ,
then
,
then
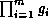 contains no convergent variables due to the second
condition of tidiness. Again the condition of Proposition
contains no convergent variables due to the second
condition of tidiness. Again the condition of Proposition 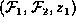 yields a
flexible heterogeneous factorization of
yields a
flexible heterogeneous factorization of 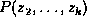 .
.
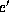 be a convergent variable in the list
be a convergent variable in the list 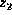 , ...,
, ..., 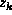 .
Then
.
Then 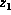 cannot be the corresponding new regular variable e.
Hence the factor
cannot be the corresponding new regular variable e.
Hence the factor 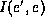 is not touched by
is not touched by
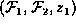 .
Consequently, if we can show that the new factor created
by
.
Consequently, if we can show that the new factor created
by 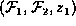 is either
a heterogeneous factor or a homogeneous factor that contain
no convergent variable, then the factorization
returned is tidy.
is either
a heterogeneous factor or a homogeneous factor that contain
no convergent variable, then the factorization
returned is tidy.
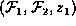 does not create a new homogeneous factor. Then no heterogeneous
factors in
does not create a new homogeneous factor. Then no heterogeneous
factors in 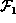 contain
contain 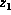 . If
. If 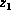 is a convergent variable, say
is a convergent variable, say 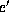 ,
then
,
then 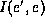 is the only homogeneous factor that
contain
is the only homogeneous factor that
contain 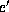 . The new factor is
. The new factor is 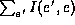 , which does
contain any convergent variables. If
, which does
contain any convergent variables. If 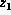 is an old regular variable
or a new regular variable whose deputy is not in the list
is an old regular variable
or a new regular variable whose deputy is not in the list
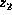 , ...,
, ..., 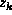 ,
all the factors that contain
,
all the factors that contain 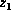 do not contain any convergent variables.
Hence the new factor again does not contain any convergent variables.
The theorem is thus proved.
do not contain any convergent variables.
Hence the new factor again does not contain any convergent variables.
The theorem is thus proved. 