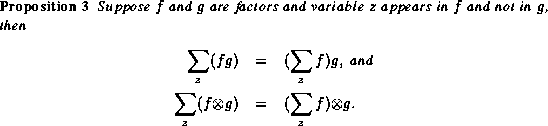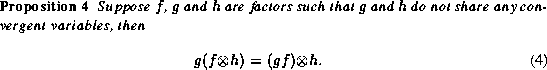Next: Rewriting Equation 2
Up: Exploiting Causal Independence in
Previous: Conditional Probabilities of
In this section, we shall first introduce an operator for combining
factors that contain convergent variables. The operator is a basic
ingredient of the algorithm to be developed in the next three
sections. Using the operator, we shall rewrite equation
(2) in a form that is more convenient to use in
inference and introduce the concept of heterogeneous factorization.
Consider two factors f and g. Let 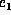 , ...,
, ..., 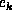 be the
convergent variables that appear in both f and g, let A be the
list of regular variables that appear in both f and g, let B
be the list of variables that appear only in f, and let C be the
list of variables that appear only in g. Both B and C can
contain convergent variables, as well as regular variables. Suppose
be the
convergent variables that appear in both f and g, let A be the
list of regular variables that appear in both f and g, let B
be the list of variables that appear only in f, and let C be the
list of variables that appear only in g. Both B and C can
contain convergent variables, as well as regular variables. Suppose
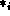 is the base combination operator of
is the base combination operator of 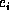 . Then, the
combination
. Then, the
combination 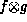 of f and g is a function of variables
of f and g is a function of variables
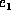 , ...,
, ..., 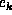 and of the variables in A, B, and C. It
is defined by:
and of the variables in A, B, and C. It
is defined by:
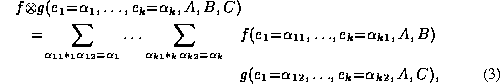
for each value 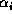 of
of 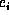 . We shall sometimes write
. We shall sometimes write
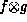 as
as 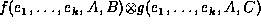 to make explicit the arguments of f and g.
to make explicit the arguments of f and g.
Note that base combination operators of different convergent variables
can be different.
The following proposition exhibits some of the basic properties of
the combination operator 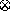 .
.
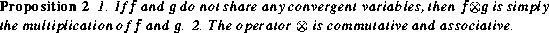
Proof:
The first item is obvious. The commutativity of
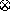 follows readily from the commutativity of multiplication and
the base combination operators.
We shall prove the associativity of
follows readily from the commutativity of multiplication and
the base combination operators.
We shall prove the associativity of 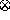 in a special
case. The general case can be proved by following the same line
of reasoning.
in a special
case. The general case can be proved by following the same line
of reasoning.
Suppose f, g, and h are three factors that contain only one
variable e and the variable is convergent. We need to show
that 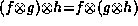 .
Let
.
Let  be the base combination operator of e.
By the associativity of
be the base combination operator of e.
By the associativity of  , we have, for any
value
, we have, for any
value  of e, that
of e, that
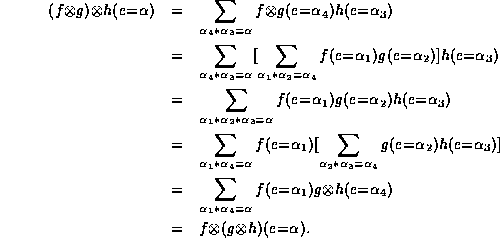
The proposition is hence proved.
The following propositions give some properties for  that
correspond to the operations that we exploited for the algorithm
that
correspond to the operations that we exploited for the algorithm 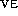 .
The proofs are straight forward and are omitted.
.
The proofs are straight forward and are omitted.
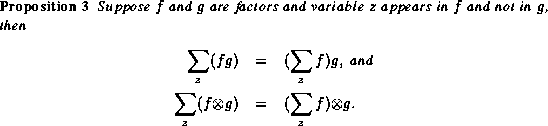
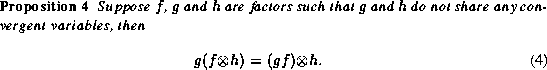



Next: Rewriting Equation 2
Up: Exploiting Causal Independence in
Previous: Conditional Probabilities of
David Poole
Fri Dec 6 15:09:32 PST 1996
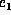 , ...,
, ..., 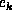 be the
convergent variables that appear in both f and g, let A be the
list of regular variables that appear in both f and g, let B
be the list of variables that appear only in f, and let C be the
list of variables that appear only in g. Both B and C can
contain convergent variables, as well as regular variables. Suppose
be the
convergent variables that appear in both f and g, let A be the
list of regular variables that appear in both f and g, let B
be the list of variables that appear only in f, and let C be the
list of variables that appear only in g. Both B and C can
contain convergent variables, as well as regular variables. Suppose
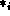 is the base combination operator of
is the base combination operator of 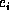 . Then, the
combination
. Then, the
combination 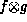 of f and g is a function of variables
of f and g is a function of variables
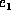 , ...,
, ..., 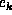 and of the variables in A, B, and C. It
is defined by:
and of the variables in A, B, and C. It
is defined by: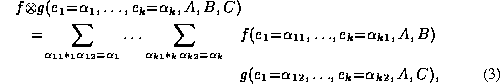
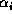 of
of 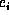 . We shall sometimes write
. We shall sometimes write
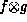 as
as 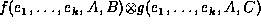 to make explicit the arguments of f and g.
to make explicit the arguments of f and g.
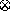 .
.
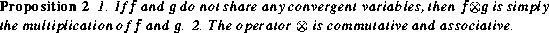
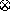 follows readily from the commutativity of multiplication and
the base combination operators.
We shall prove the associativity of
follows readily from the commutativity of multiplication and
the base combination operators.
We shall prove the associativity of 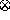 in a special
case. The general case can be proved by following the same line
of reasoning.
in a special
case. The general case can be proved by following the same line
of reasoning.
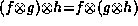 .
Let
.
Let  be the base combination operator of e.
By the associativity of
be the base combination operator of e.
By the associativity of  , we have, for any
value
, we have, for any
value  of e, that
of e, that
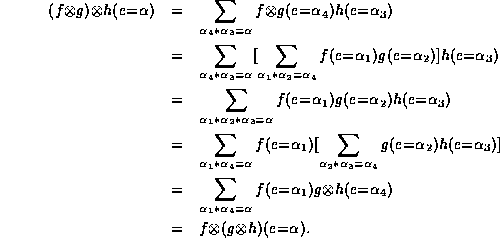

 that
correspond to the operations that we exploited for the algorithm
that
correspond to the operations that we exploited for the algorithm  .
The proofs are straight forward and are omitted.
.
The proofs are straight forward and are omitted.