|
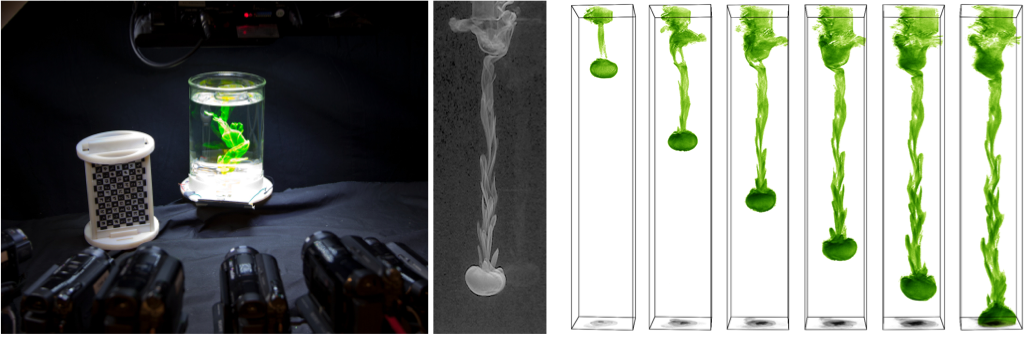
Using an array of consumer video cameras (left) we obtain multiple views (center) of a fluorescing fluid mixing with a transparent fluid. By assuming an emissive image formation model, we are able to cast the problem of reconstructing the fluorescing fluid as a tomographic reconstruction problem. We solve this problem using a novel particle-based Stochastic Tomography algorithm that is grid- and matrix-free and produces a sample set with density proportional to the desired emissivity field (right). The Stochastic Tomography algorithm is inspired by Metropolis-Hastings sampling and avoids many problems commonly associated with tomographic reconstruction by being automatically adaptive, able to incorporate nearly arbitrary regularization schemes and able to simultaneously reconstruct and re-render volume data without ever actually storing a volume.
Abstract
We present a novel approach for highly detailed 3D imaging of turbulent fluid mixing behaviors. The method is based on visible light computed tomography, and is made possible by a new stochastic tomographic reconstruction algorithm based on random walks similar to Metropolis sampling. We show that this new stochastic algorithm is competitive with specialized tomography solvers such as SART, but can also easily include arbitrary convex regularizers that make it possible to obtain high-quality reconstructions with a very small number of views. Finally, we demonstrate that the same stochastic tomography approach can also be used to directly re-render arbitrary 2D projections without the need to ever store a 3D volume grid.
|
|
Paper and Video
Citation
@article{StochasticTomography-Gregson2012,
author = {James Gregson and Michael Krimerman and Matthias B. Hullin and Wolfgang Heidrich},
title = {Stochastic Tomography and its Applications in 3D Imaging of Mixing Fluids},
journal = {ACM Trans. Graph. (Proc. SIGGRAPH 2012)},
volume = {31},
number = {4},
year = {2012},
pages = {52:1--52:10 (to appear)},
}
|
Results
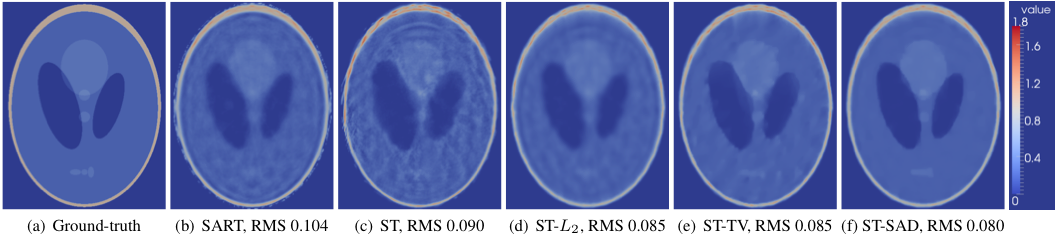 |
2D results for the Shepp-Logan phantom from 16 synthetic cameras with identical compute times. Note that this is a challenging test due to the very small number of projections. Ground truth (a), SART reconstruction (b), basic Stochastic Tomography (c), L2-regularized Stochastic tomography (d), Total Variation regularized Stochastic Tomography and Sum-of-Absolute-Differences (SAD) regularized Stochastic Tomography. Without regularization the Stochastic Tomography algorithm produces noisier results than SART, however this improves drastically when regularizers are introduced. We have found that the SAD regularizer is particularly effective, producing high-quality results with negligible impact on runtimes. The ability to incorporate effectively arbitrary regularizers into the algorithm is a key advantage of Stochastic Tomography, allowing domain-specific knowledge to be exploited quickly and easily.
|
 |
Reconstruction at varying levels of completion, points plot the last 10k accepted samples, blue points are positive samples, red points negative. The method first 'roughs-in' the reconstruction, then refines details. Please see the paper and video for more details.
|
 |
Reconstructions at various times of the turbulent mixing of a fluorescing dye poured into still water.
|
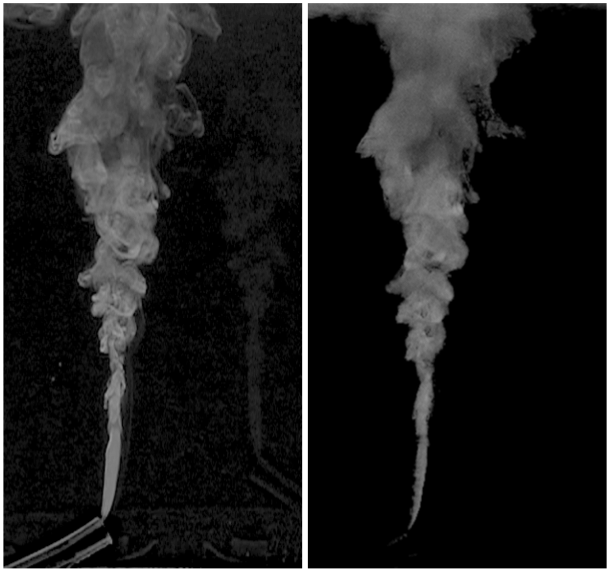 |
Comparison of experiment with reconstruction by Stochastic Tomography of fluorescing alcohol rising under buoyancy and transitioning from laminar to turbulent flow. Captured data (left) and grid-free reconstruction by Stochastic Tomography (right) from a similar projection. Stochastic Tomography captures many of the small-scale features of this laminar-to-turbulent transistion.
|
Datasets
Here we provide a sampling of the datasets that were used for this paper. Full datasets are available on request however are not being made directly downloadable due to hosting constraints. Please contact us if you would like to obtain the complete sets. Please see the dataset description file for an outline of the directory structure/files and calibration procedures used in this project before downloading the data.
All images are © ACM, 2012, reproduced here by permission of ACM for your personal use. Not for redistribution. Some of the source graphics on which these works were based are copyrighted by third parties and used with their permission. See the Acknowledgements section of our paper for a list of third-party sources.




