Time-resolved 3D Capture of Non-stationary
Gas Flows

Bradley Atcheson1, Ivo Ihrke1, Wolfgang Heidrich1, Art Tevs2,
Derek Bradley1, Marcus Magnor3, Hans-Peter Seidel2

1. The University of British Columbia
2. Max-Planck-Institut für Informatik
3. Braunschweig University

     

SIGGRAPH Asia 2008


Download:    PDF    AVI   

Bibtex:
@ARTICLE{Atcheson:2008,
   author = {Bradley Atcheson and Ivo Ihrke and Wolfgang Heidrich and Art Tevs and Derek Bradley and Marcus Magnor and Hans-Peter Seidel},
   title = {Time-resolved 3D Capture of Non-stationary Gas Flows},
   journal = {ACM Transactions on Graphics (Proc. SIGGRAPH Asia)},
   year = {2008},
   volume = {27},
   number = {5},
   pages = {132},
}


Abstract

Fluid simulation is one of the most active research areas in computer graphics. However, it remains difficult to obtain measurements of real fluid flows for validation of the simulated data.

In this paper, we take a step in the direction of capturing flow data for such purposes. Specifically, we present the first time-resolved Schlieren tomography system for capturing full 3D, non-stationary gas flows on a dense volumetric grid. Schlieren tomography uses 2D ray deflection measurements to reconstruct a time-varying grid of 3D refractive index values, which directly correspond to physical properties of the flow. We derive a new solution for this reconstruction problem that lends itself to efficient algorithms to robustly work with relatively small numbers of cameras. Our physical system is easy to set up, and consists of an array of relatively low cost rolling-shutter camcorders that are synchronized with a new approach. We demonstrate our method with real measurements, and analyze precision with synthetic data for which ground truth information is available.


Overview


Acquisition
Raw data is captured by an array of 16 independent HD camcorders. Static background patterns placed behind the volume are imaged through a gas flow. We employ a novel synchronisation scheme to obtain time-varying multi-view measurements from the rolling-shutter cameras.
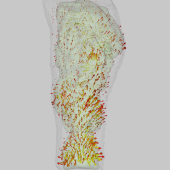
2D deflection sensing
Refraction occurs due to gas density inhomogeneities inside the flow.The resulting per-pixel deflections are captured with an optical flow algorithm.
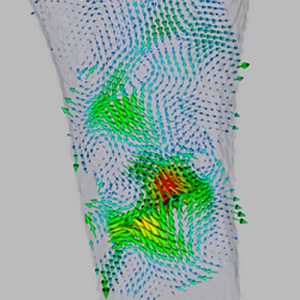Gradient field tomography
Given the measured 2D displacement vectors, and the known experimental configuration, we can approximate 3D displacement vectors. From these we tomographically obtain the 3D refractive index gradient field.
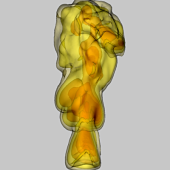
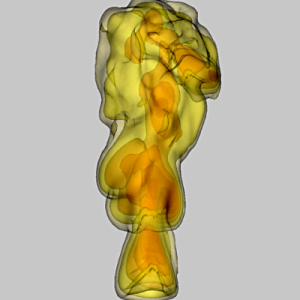
Gradient field integration
From the reconstructed gradient vectors we solve the associated Poisson equation to obtain the scalar refractive index field. In many cases, this provides an approximation of the temperature distribution.

Results



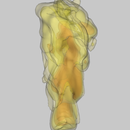
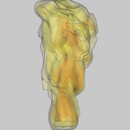
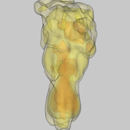
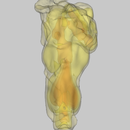
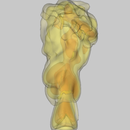
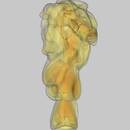
Camping stove



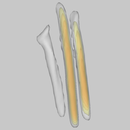
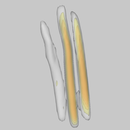
Candles