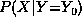 of a set X of query variables
after obtaining some observations
of a set X of query variables
after obtaining some observations 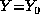 . Here Y is a list of
observed variables and
. Here Y is a list of
observed variables and 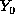 is the corresponding list of
observed values. Often, X consists of only one query variable.
is the corresponding list of
observed values. Often, X consists of only one query variable.
Inference refers to the process of computing the posterior
probability 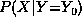 of a set X of query variables
after obtaining some observations
of a set X of query variables
after obtaining some observations 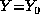 . Here Y is a list of
observed variables and
. Here Y is a list of
observed variables and 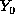 is the corresponding list of
observed values. Often, X consists of only one query variable.
is the corresponding list of
observed values. Often, X consists of only one query variable.
In theory, 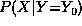 can be obtained from
the marginal probability
can be obtained from
the marginal probability
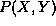 , which in turn can be computed from the joint probability
, which in turn can be computed from the joint probability
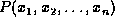 by summing out variables outside
by summing out variables outside 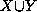 one by one. In practice, this is not viable
because summing out a variable from a joint probability requires
an exponential number of additions.
one by one. In practice, this is not viable
because summing out a variable from a joint probability requires
an exponential number of additions.
The key to more efficient inference lies in the concept of factorization. A factorization of a joint probability is a list of factors (functions) from which one can construct the joint probability.
A factor is a function from a set of variables into a number.
We say that the factor contains a variable if the factor is a function
of that variable; or say it is a factor of the variables on
which it depends. Suppose 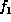 and
and 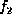 are factors, where
are factors, where 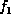 is a factor that contains variables
is a factor that contains variables
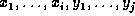 --- we write this as
--- we write this as
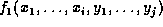 --- and
--- and 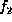 is a factor with
variables
is a factor with
variables 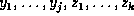 , where
, where 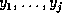 are
the variables in common to
are
the variables in common to 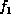 and
and 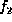 . The product of
. The product of 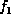 and
and
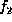 is a factor that is a function of the union of the variables,
namely
is a factor that is a function of the union of the variables,
namely 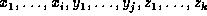 , defined by:
, defined by:
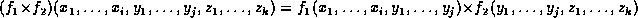
Let 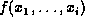 be a function of variable
be a function of variable 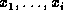 .
Setting, say
.
Setting, say 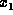 in
in 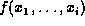 to a particular value
to a particular value  yields
yields
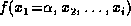 , which is a function of variables
, which is a function of variables 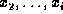 .
.
If 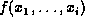 is a factor, we can sum out a variable, say
is a factor, we can sum out a variable, say 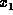 , resulting in a factor of variables
, resulting in a factor of variables 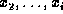 , defined
, defined
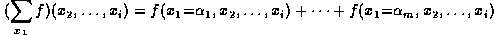
where 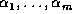 are the possible values of variable
are the possible values of variable 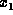 .
.
Because of equation (1), a BN
can be viewed as representing a factorization of
a joint probability.
For example, the Bayesian network in Figure 1
factorizes the joint probability 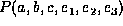 into the following list of factors:
into the following list of factors:
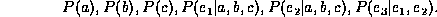
Multiplying those factors yields the joint probability.
Suppose a joint probability 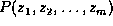 is factorized into the multiplication of
a list of factors
is factorized into the multiplication of
a list of factors 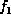 ,
, 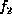 , ...,
, ..., 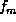 .
While obtaining
.
While obtaining 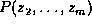 by summing out
by summing out 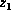 from
from 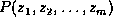 requires an exponential number of additions,
obtaining a factorization of
requires an exponential number of additions,
obtaining a factorization of 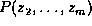 can often be done
with much less computation.
Consider the following procedure:
can often be done
with much less computation.
Consider the following procedure:
Proceduresum-out:
- Inputs:
--- a list of factors; z --- a variable.
- Output: A list of factors.
- Remove from the
all the factors, say
, ...,
, that contain z,
- Add the new factor
to
and return
.
Proof:
Suppose 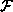 consists of factors
consists of factors
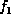 ,
, 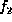 , ...,
, ..., 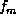 and suppose
and suppose
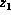 appears in and only in factors
appears in and only in factors
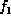 ,
, 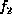 , ...,
, ..., 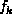 . Then
. Then
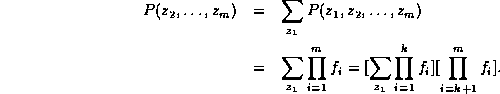
The theorem follows. 
Only variables that appear in the factors 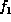 ,
, 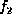 , ...,
, ..., 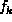 participated in the computation of
participated in the computation of
sum-out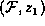 , and those are often only a small
portion of all the variables.
This is why inference in a BN can be tractable in many cases, even if the
general problem is NP-hard [5].
, and those are often only a small
portion of all the variables.
This is why inference in a BN can be tractable in many cases, even if the
general problem is NP-hard [5].