Go backward to 2 Independence Entailed by a Belief Networks
Go up to Top
Go forward to 4 Variable Elimination Algorithm (Multiply Connected)

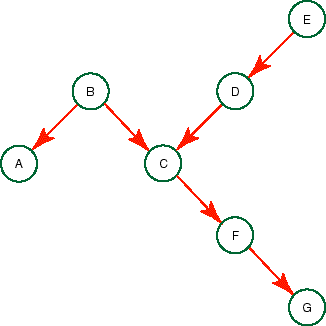
3 Variable Elimination Algorithm (Singly Connected)

In this question we trace through one instance of the variable elimination algorithm for a singly connected belief net (i.e., if we ignore the arc directions, there is at most one path between any two nodes).

Consider the following belief network:

Assume that all of the variables are Boolean (i.e., have domain {true,false}.

We will write variables in upper case, and use lower-case letters for the corresponding propositions. In particular, we will write A=true as a and A=false as ¬a, and similarly for the other variables.

Suppose we have the following conditional probability tables:

P(a|b)=0.88
P(a|¬ b)=0.38
P(b) = 0.7
P(c|b& d)=0.93
P(c| b& ¬ d)=0.33
P(c|¬ b& d)=0.53
P(c|¬ b& ¬ d)=0.83
P(d|e)=0.04
P(d|¬ e)=0.84
P(e) = 0.91
P(f|c)=0.45
P(f|¬ c)=0.85
P(g|f)=0.26
P(g|¬ f)=0.96

We will draw the factors as tables. The above conditional probability tables are all we need to build the factors. For example, the factor representing P(E) can be written as:

E Value

true 0.91

false 0.09

The factor for P(D|E) can be written as

E D Value

true true 0.04

true false 0.96

false true 0.84

false false 0.16

and similarly for the other factors.

In this question you are to consider the following elimination steps in order (i.e., assume that the previous eliminations and observations have been carried out). We want to compute P(A|g). (Call your created factors f₁, f₂, etc.)

Suppose we first eliminate the variable E. Which factor(s) are removed, and show the complete table for the factor that is created. Show explicitly what numbers were multiplied and added to get your answer.
Suppose we were to eliminate D. What factor(s) are removed and which factor is created. Give the table for the created factor.
Suppose we were to observe g (i.e., observe G=true). What factor(s) are removed and what factor(s) are created?
Suppose we now eliminate F. What factor(s) are removed, and what factor is created?
Suppose we now eliminate C. What factor(s) are removed, and what factor is created?
Suppose we now eliminate B. What factor(s) are removed, and what factor is created?
What is the posterior probability distribution of E? What is the prior probability of the observations?
For each factor created, can you give an interpretation of what the function means?