The algorithms are described in the following paper:
cd UGMlearn addpath(genpath(pwd)) mexAll example_groupL1 % example of Group L1-Regularziation example_UGMlearn(0) % example of Undirected Parameter/Structure learning methods example_UGMlearn(1) % the same example, but showing the graphs (requires graphviz)
The script 'example_groupL1.m' generates a synthetic linear regression data set, and displays the Least Squares regularization path with L1-regularization, Group L1-regularization with the 2-norm, and Group L1-regularization with the infinity-norm (the script waits for the user to press a key between running the different methods).
The script 'example_UGMlearn.m' generates a synthetic conditional random field (CRF) data set, and runs the different parameter/structure learning methods from the paper on it. If called as 'example_UGMlearn(0)', it displays the test error produced by each method. If graphviz is installed, it can be called as 'example_UGMlearn(1)', and will display both the test error and final graph structures.
nInstances = 100; % Number of training examples p = 15; % Number of variables lambda = 500; % Strength of regularizer % Make vector containing group memberships (note: Group 0 is reserved for non-regularized variables groups = zeros(p,1); groups(1:3:p) = [1:p/3]'; groups(2:3:p) = [1:p/3]'; groups(3:3:p) = [1:p/3]'; nGroups = length(unique(groups(groups>0))); % Generate Data X = randn(nInstances,p); % Generate Random Features wTrue = randn(p,1).*groups; % Generate Random Weights, where higher groups have higher weight multiplier y = X*wTrue + randn(nInstances,1); % Generate labels as linear combination plus random noise funObj_sub = @(w)GaussianLoss(w,X,y); % We will be minimizing the Least Squares lost
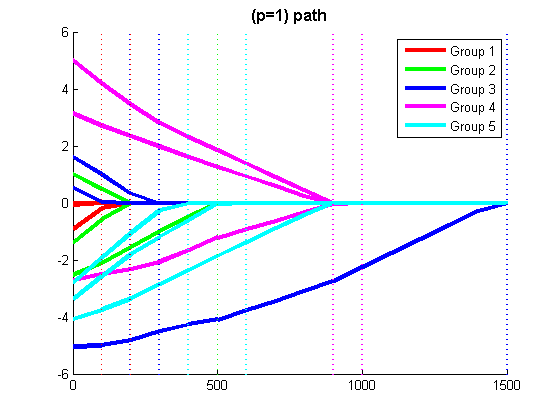
% Code to optimize funObj_sub with L1-regularization lambdaVect = lambda*ones(p,1); % Vector of regularization parameters (one for each variable) funObj = @(w)nonNegGrad(w,lambdaVect,funObj_sub); % Surrogate objective function that divides variables into non-negative parts wPosNeg = minConF_BC(funObj,zeros(2*p,1),zeros(2*p,1),inf(2*p,1)); % Solve non-negatively constrained optimization problem w = wPosNeg(1:p)-wPosNeg(p+1:end) % Put non-negative parts together to get final anwser
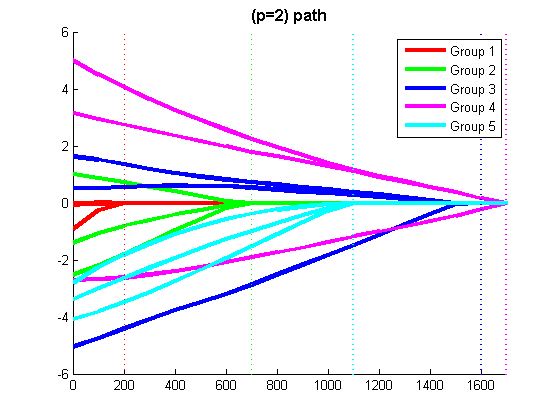
% Code to optimize funObj_sub with Group L1-regularization (L1-regularization of group 2-norms) % Make Auxiliary variable Objective and Projection Function funObj = @(w)auxGroupLoss(w,groups,lambda,funObj_sub); funProj = @(w)auxGroupL2Proj(w,groups); % Solve wAlpha = minConF_SPG(funObj,zeros(p+nGroups,1),funProj); w = wAlpha(1:p) % Remove auxiliary variables
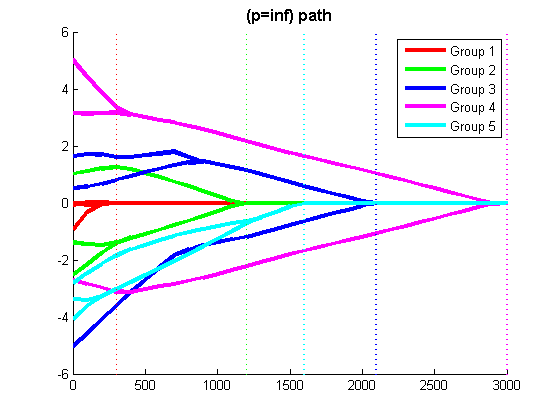
% Code to optimize funObj_sub with Group L1-regularization (L1-regularization of group infinity-norms) % Make Auxiliary variable Objective and Projection Function funObj = @(w)auxGroupLoss(w,groups,lambda,funObj_sub); funProj = @(w)auxGroupLinfProj(w,groups); % Solve wAlpha = minConF_SPG(funObj,zeros(p+nGroups,1),funProj); w = wAlpha(1:p) % Remove auxiliary variables
nTrain = 500; % number of examples to use for training nTest = 1000; % number of examples to use for testing nFeatures = 10; % number of features for each node nNodes = 10; % number of nodes nStates = 2; % number of states that each node can takeThe nTrain parameter specifies the number of examples to generate for training the CRF, and the nTest parameter specifies the number of examples used to evaluate its classification performance. The nFeatures parameter specifies the number of features associated with each node (in addition to the bias), it can be set to 0 in order to generate a Markov Random Field (MRF) instead of a CRF. nStates specifies the number of states that each node can take.
edgeProb = .5; % probability of each edge being included in the graph edgeType = 1; % set to 0 to make the edge features normally distributed ising = 0; % set to 1 to use ising potentialsedgeProb specifies the probability that each edge is included in the underlying graph. Setting edgeType to 0 makes the edge parameters in the underlying graph normally distributed, and setting it to 1 makes the edge parameters uniformly distributed within an interval, where the interval size is normally distributed across the edges. Setting ising to 1 will use Ising-like potentials, while setting it to 0 will use full pairwise potentials.
trainType = 'pseudo'; % set to 'pseudo' for pseudo-likelihood, 'loopy' for loopy belief propagation, 'exact' for 'exact inference testType = 'exact'; % set to 'loopy' to test with loopy belief propagation, 'exact' for exact inference structureSeed = 0; % change this to generate different structures trainSeed = 0; % vary seed from 0:9 to get paper results useMex = 1; % use mex files in UGM to speed things uptrainType can be set to 'pseudo' for training with pseudo-likelihood, 'loopy' for pseudo-moment matching with loopy belief propagation, or 'exact' for exact training (only suitable for up to ~16 nodes). testType can be set to 'exact' to use exact inference when testing (only suitable for up to ~16 nodes), and 'loopy' to test using loopy belief propagation for approximate inference. structureSeed is the seed passed to the random number generator when computing the graph structure, and trainSeed is the seed used when splitting the data into training and testing examples (the values 0:9 were used in the paper). Finally, setting useMex to 1 turns on the use of mex files to speed up parts of the computation in the UGM code, while setting it to 0 will exclusively use Matlab code.
% Regularization Parameters lambdaNode = 10; lambdaEdge = 10;These two parameters affect the strength of the regularizer. While the demo uses fixed values, in the paper we picked these values by two-fold cross-validation, testing the values 2.^[7:-1:-5], using warm-starting to speed up the optimization for this sequence of values.
%% Generate data nInstances = nTrain+nTest; [y,adjTrue,X] = UGM_generate(nInstances,nFeatures,nNodes,edgeProb,nStates,ising,tied,useMex,edgeType); perm = randperm(nInstances); trainNdx = perm(1:nTrain); testNdx = perm(nTrain+1:end);This code generates the synthetic CRF data, and splits it into training and testing examples.
%% Fixed Structure Methods edgePenaltyType = 'L2'; % Empty Structure type = 'Fixed: Empty'; adjInit = zeros(nNodes); example_UGMlearnSub;This code specifies that the edges are regularized with L2-regularization, and that the initial adjacency matrix is empty. example_UGMlearnSub.m is a script that trains and tests the CRF. The other 'Fixed Structure' and 'Generative Non-L1' methods are run by changing the adjInit matrix.
%% Generative L1 Methods % Regular L1 type = 'Generative L1: L1-L1'; edgePenaltyType = 'L1'; % Train with L1 regularization on the edges Xold = X; X = zeros(nInstances,0,nNodes); % Train while ignoring features adjInit = fixed_Full(nNodes); example_UGMlearnSub adjInit = adjFinal; X = Xold; edgePenaltyType = 'L2'; subDisplay = display; example_UGMlearnSubFor the 'Generative-L1' methods, we first train a full CRF that ignores the features and uses (group) L1-regularization in order to learn the graph structure. We then use this structure to train the final CRF that incorporates the features.
%% Discriminative L1 Methods type = 'Discriminative L1: L1-L1'; edgePenaltyType = 'L1'; % Train with L1 regularization on the edges adjInit = fixed_Full(nNodes); example_UGMlearnSubFor the 'Discriminative-L1' methods, we train a full CRF that uses the features and (group) L1-regularization in order to learn the parameters and graph structure at the same time.
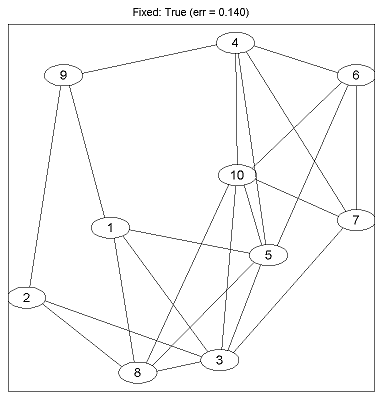
Generating Synthetic CRF Data... Exact Sampling Training Fixed: Empty... Error Rate (Fixed: Empty): 0.266 Training Fixed: Chain... Error Rate (Fixed: Chain): 0.250 Training Fixed: Full... Error Rate (Fixed: Full): 0.184 Training Fixed: True... Error Rate (Fixed: True): 0.140 Training Generative Non-L1: Tree... Error Rate (Generative Non-L1: Tree): 0.220 Training Generative Non-L1: DAG... Error Rate (Generative Non-L1: DAG): 0.224 Training Generative L1: L1-L1... Error Rate (Generative L1: L1-L1): 0.204 Training Generative L1: L1-L2... Error Rate (Generative L1: L1-L2): 0.202 Training Generative L1: L1-Linf... Error Rate (Generative L1: L1-Linf): 0.192 Training Discriminative L1: L1-L1... Error Rate (Discriminative L1: L1-L1): 0.180 Training Discriminative L1: L1-L2... Error Rate (Discriminative L1: L1-L2): 0.150 Training Discriminative L1: L1-Linf... Error Rate (Discriminative L1: L1-Linf): 0.178Running the demo as 'example_UGMlearn(1)' will show the progress of the optimization algorithms and also pauses to show the final graph structure after each method is run. Below is the graph produced under the true generating structure: