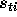 and the computed probability
and the computed probability
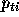 for that output label based on its nearest neighbours:
for that output label based on its nearest neighbours:
The similarity metric weights and the kernel width factor are optimized using the cross-validation procedure that has been widely adopted in neural network research. This minimizes the error resulting when the output of each exemplar in the training set is predicted on the basis of the remaining data without that exemplar. As Atkeson (1991) has discussed, this is simple to implement with the nearest-neighbour method because it is trivial to ignore one data item when applying the interpolation kernel. This avoids some of the problems of overtraining that are found in many other neural network learning methods that can not so easily remove a single exemplar to measure the cross validation error.
The particular optimization technique that has been used is conjugate gradient (with the Polak-Ribiere update), because it is efficient even with large numbers of parameters and converges rapidly without the need to set convergence parameters. One important technique in applying it to this problem is that the set of neighbours of each exemplar are stored before each line search, and the same neighbours are used throughout the line search. This avoids introducing discontinuities to the error measure due to changes in the set of neighbours with a changing similarity metric, which could lead in turn to inappropriate choices of step size in the line search. A nice side-effect is that this greatly speeds the line search, as repeatedly finding the nearest neighbours would otherwise be the dominant cost. For the problems we have studied, the conjugate gradient method converges to a minimum error in about 5 to 20 iterations.
In order to apply the conjugate gradient optimization in an efficient
manner, it is necessary to compute the derivative of the cross
validation error with respect to the parameters being optimized.
The cross validation error E is defined as the sum over all training
exemplars t and output labels i of the squared difference
between the known correct output 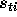 and the computed probability
and the computed probability
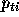 for that output label based on its nearest neighbours:
for that output label based on its nearest neighbours:
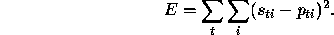
The derivative of this error can be computed with respect to each
weight parameter 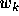 :
:
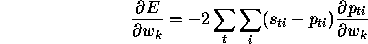
where
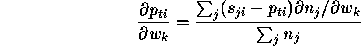
and
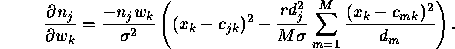
The sum in this last expression does not depend on the particular neighbour j and can therefore be precomputed for the set of neighbours.
In order to optimize the parameter r determining the width of the Gaussian kernel, we can substitute the derivative with respect to r for the last equation above:

As noted above, the error function has discontinuities whenever the set of nearest neighbours changes due to changing weights. This can lead to inappropriate selection of the conjugate gradient search direction, so the search direction should be restarted (i.e., switched to pure gradient descent for the current iteration) whenever the error or the gradient increases. In fact, simple gradient descent with line search seems to work well for this problem, with only a small increase in the number of iterations required as compared to conjugate gradient.
One final improvement to the optimization process is to add a stabilizing term to the error measure E that can be used to prevent large weight changes when there is only a small amount of training data. This is less important than for most other neural network methods because of the smaller number of parameters, but it can still be useful for preventing overfitting to small samples of noisy training data. The following stabilizing term S is added to the cross-validation error E:
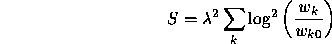
which has a derivative of
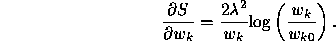
This tends to keep the value of each weight 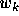 as close as possible
to the initial weight value
as close as possible
to the initial weight value 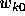 assigned by the user prior to
optimization. We have used the stabilization constant
assigned by the user prior to
optimization. We have used the stabilization constant 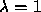 ,
which means that a one log-unit change in the weight carries a
penalty equivalent to a complete misclassification of a single item of
training data. This has virtually no effect when there is a large
amount of training data---as in the NETtalk problem below---but will
prevent large weight changes based on a statistically invalid sample
for small data sets.
,
which means that a one log-unit change in the weight carries a
penalty equivalent to a complete misclassification of a single item of
training data. This has virtually no effect when there is a large
amount of training data---as in the NETtalk problem below---but will
prevent large weight changes based on a statistically invalid sample
for small data sets.