


Next: Optimization of the
Up: Similarity Metric Learning for
Previous: Previous research
The choice of the interpolating kernel can have a substantial effect
on the performance of a nearest-neighbours classifier. Cover & Hart
(1967) showed that the single nearest-neighbour rule can have
twice the error rate of a kernel that obtains an accurate measure of
the local Bayes probability. A doubling of the error rate for
a given set of training data would make even the best learning method
appear to have poor performance relative to the alternatives.
One widely-used kernel is to place a fixed-width Gaussian at each
neighbour, as in the Parzen window method. However, a fixed-width
kernel will be too small to achieve averaging where data points are
sparse and too large to achieve optimal locality where data points are
dense. There is a trade-off between averaging points to achieve a
better estimate of the local Bayes probability versus maintaining
locality in order to capture changes in the output. As Duda & Hart
(1973, p. 105) have shown, most of the benefits of local averaging
are achieved from averaging small numbers of points. In fact, the
k-nearest-neighbour method achieves a relatively good performance by
maintaining a constant number of points within the kernel.
The benefits of the k-nearest-neighbour method can be combined with
the smooth weighting fall-off of a Gaussian by using what is known as
the variable kernel method (Silverman, 1986). In this method, the
size of a Gaussian kernel centered at the input is set proportional to
the distance of the k-th nearest neighbour. In this paper, we
instead use the average distance of the first k neighbours, because
this measure is more stable under a changing similarity metric. The
constant relating neighbour distance to the Gaussian width is learned
during the optimization process, which allows the method to find the
optimal trade-off between localization and averaging for each
particular data set.
In a classification problem, the objective is to compute a probability
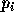 for each possible output label i given any new input vector
for each possible output label i given any new input vector
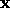 . In VSM learning, this is done by taking the weighted
average of the known correct outputs of a number of nearest
neighbours. Let
. In VSM learning, this is done by taking the weighted
average of the known correct outputs of a number of nearest
neighbours. Let 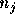 be the weight that is assigned to each of the
J (e.g., J=10) nearest neighbours, and
be the weight that is assigned to each of the
J (e.g., J=10) nearest neighbours, and 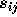 be the known
output probability (usually 0 or 1) for label i of each neighbour. Then,
be the known
output probability (usually 0 or 1) for label i of each neighbour. Then,

The weight 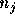 assigned to each neighbour is determined by a
Gaussian kernel centered at
assigned to each neighbour is determined by a
Gaussian kernel centered at 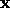 , where
, where 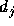 is the distance of
the neighbour from
is the distance of
the neighbour from 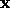 :
:

The distance 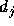 depends on the similarity metric weights
depends on the similarity metric weights 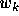 that
will be learned during the optimization process for each dimension
k of the input vector. Let
that
will be learned during the optimization process for each dimension
k of the input vector. Let  be the input location of each
neighbour. Then, the weighted Euclidean distance is
be the input location of each
neighbour. Then, the weighted Euclidean distance is
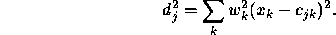
The width of the Gaussian kernel is determined by  , which is a
multiple of the average distance to the M nearest neighbours. It is
better if only some fraction (e.g.,
, which is a
multiple of the average distance to the M nearest neighbours. It is
better if only some fraction (e.g., 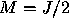 ) of the neighbours is
used, so that the kernel becomes small even when only a few neighbours
are close to the input. There is a multiplicative parameter r
relating the average neighbour distance to
) of the neighbours is
used, so that the kernel becomes small even when only a few neighbours
are close to the input. There is a multiplicative parameter r
relating the average neighbour distance to  which is learned
as a part of the optimization process (a typical initial value is
which is learned
as a part of the optimization process (a typical initial value is
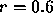 , which places the average neighbour near the steepest slope of
the Gaussian):
, which places the average neighbour near the steepest slope of
the Gaussian):

If it is successful, the optimization will select a larger value for
r for noisy but densely-sampled data, and a smaller value for data
that is sparse relative to significant variations in output.



Next: Optimization of the
Up: Similarity Metric Learning for
Previous: Previous research
David Lowe
Wed Jul 16 17:08:22 PDT 1997
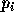 for each possible output label i given any new input vector
for each possible output label i given any new input vector
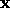 . In VSM learning, this is done by taking the weighted
average of the known correct outputs of a number of nearest
neighbours. Let
. In VSM learning, this is done by taking the weighted
average of the known correct outputs of a number of nearest
neighbours. Let 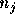 be the weight that is assigned to each of the
J (e.g., J=10) nearest neighbours, and
be the weight that is assigned to each of the
J (e.g., J=10) nearest neighbours, and 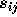 be the known
output probability (usually 0 or 1) for label i of each neighbour. Then,
be the known
output probability (usually 0 or 1) for label i of each neighbour. Then,

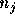 assigned to each neighbour is determined by a
Gaussian kernel centered at
assigned to each neighbour is determined by a
Gaussian kernel centered at 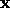 , where
, where 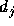 is the distance of
the neighbour from
is the distance of
the neighbour from 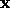 :
:

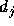 depends on the similarity metric weights
depends on the similarity metric weights 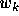 that
will be learned during the optimization process for each dimension
k of the input vector. Let
that
will be learned during the optimization process for each dimension
k of the input vector. Let  be the input location of each
neighbour. Then, the weighted Euclidean distance is
be the input location of each
neighbour. Then, the weighted Euclidean distance is
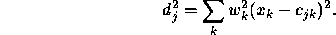
 , which is a
multiple of the average distance to the M nearest neighbours. It is
better if only some fraction (e.g.,
, which is a
multiple of the average distance to the M nearest neighbours. It is
better if only some fraction (e.g., 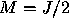 ) of the neighbours is
used, so that the kernel becomes small even when only a few neighbours
are close to the input. There is a multiplicative parameter r
relating the average neighbour distance to
) of the neighbours is
used, so that the kernel becomes small even when only a few neighbours
are close to the input. There is a multiplicative parameter r
relating the average neighbour distance to  which is learned
as a part of the optimization process (a typical initial value is
which is learned
as a part of the optimization process (a typical initial value is
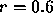 , which places the average neighbour near the steepest slope of
the Gaussian):
, which places the average neighbour near the steepest slope of
the Gaussian):
