Tumor growth models
Computational models of tumor growth form a contemporary area of study. Diffuse interface models have been recently proposed as a tool with an important significance to cancer modeling. In this project, we considered preconditioners for numerical simulations of diffuse interface tumor growth problems.
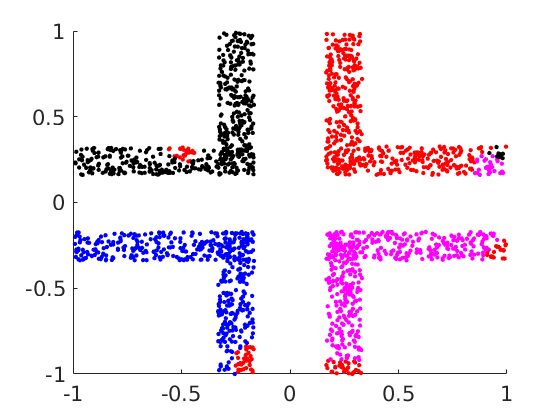
Classification of high-dimensional data on graphs
Diffuse interface methods have recently been introduced by Bertozzi et al. for the task of semi-supervised learning in the graph domain. We generalized the previously proposed model by a nonsmooth potential function. Additionally, we showed that the diffuse interface method can be used for the segmentation of data coming from hypergraphs. This project was in collaboration with Martin Stoll and Steffen Klamt.

Two-phase flows
We developed preconditioners for the solution of a fully coupled two-component Cahn-Hilliard Navier-Stokes system. Such a model is used for the numerical simulation of two-phase flows. The figure below illustrates a simulation of a rising bubble.
Abels et al. introduced the diffuse interface model for two-phase flows of two incompressible fluids with different densities. Garcke et al. developed a special time and space discretization scheme for this model, which conserves the energy inequality. Our contribution was the iterative solution of the arising linear systems. This is based on the preconditioning techniques we have developed for the Cahn-Hilliard model (described below) together with the methods that have been developed for the Navier-Stokes equations. This project was in collaboration with Martin Stoll and Christian Kahle.
Phase field solvers
Phase field models are used to solve interfacial problems. The Cahn-Hilliard equation belongs to the class of phase field models. We studied efficient numerical solution techniques for various types of Cahn-Hilliard problems. Originally, the Cahn-Hilliard equation was introduced to model phase separation in two-component alloys. In praxis, often more than two components occur, and the model has been extended to the multi-component case.
The underlying energy functional includes a potential for which different types were proposed in the past. We considered smooth and nonsmooth potentials with a focus on the latter. Whereas the use of smooth potentials leads to a system of parabolic PDEs, the nonsmooth ones result in a system of variational inequalities. In order to deal with the variational inequalities, we applied a function space-based algorithm, which combines a Moreau-Yosida regularization technique with a semismooth Newton method. We applied classical finite element methods to discretize the problems in space. The core of our approach was the solution of the arising large and sparse fully discrete systems of linear equations. We developed efficient practical preconditioners for the iterative solution of the linear systems. In particular, our preconditioners are tailored to the Cahn-Hilliard problems. We developed block preconditioners using effective Schur complement approximations.

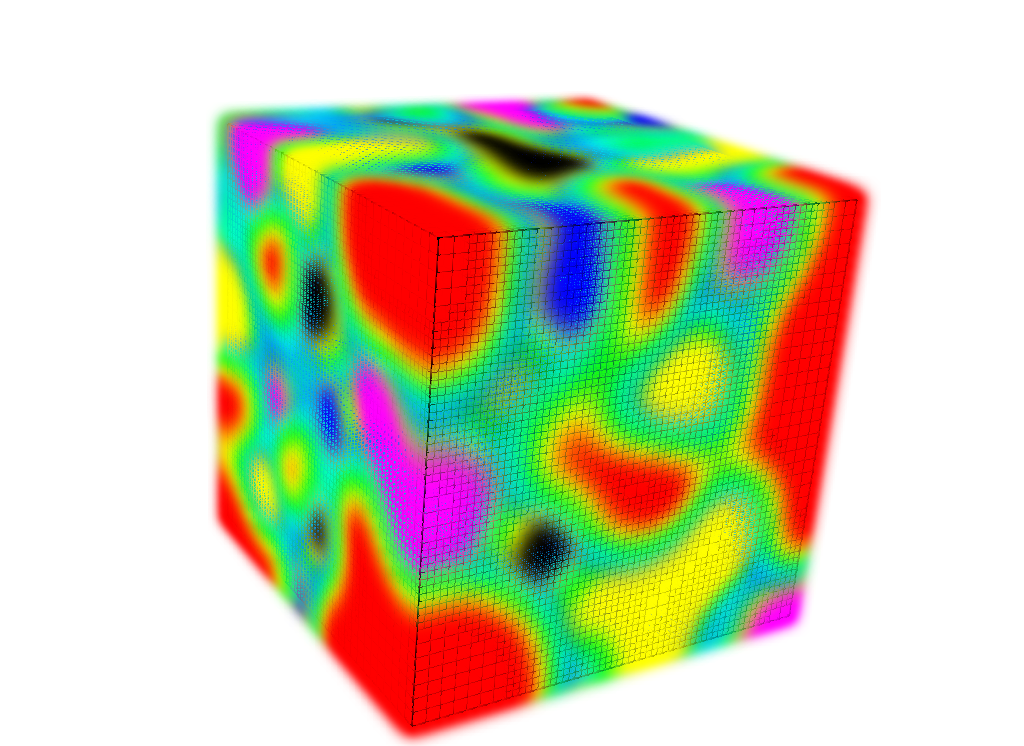
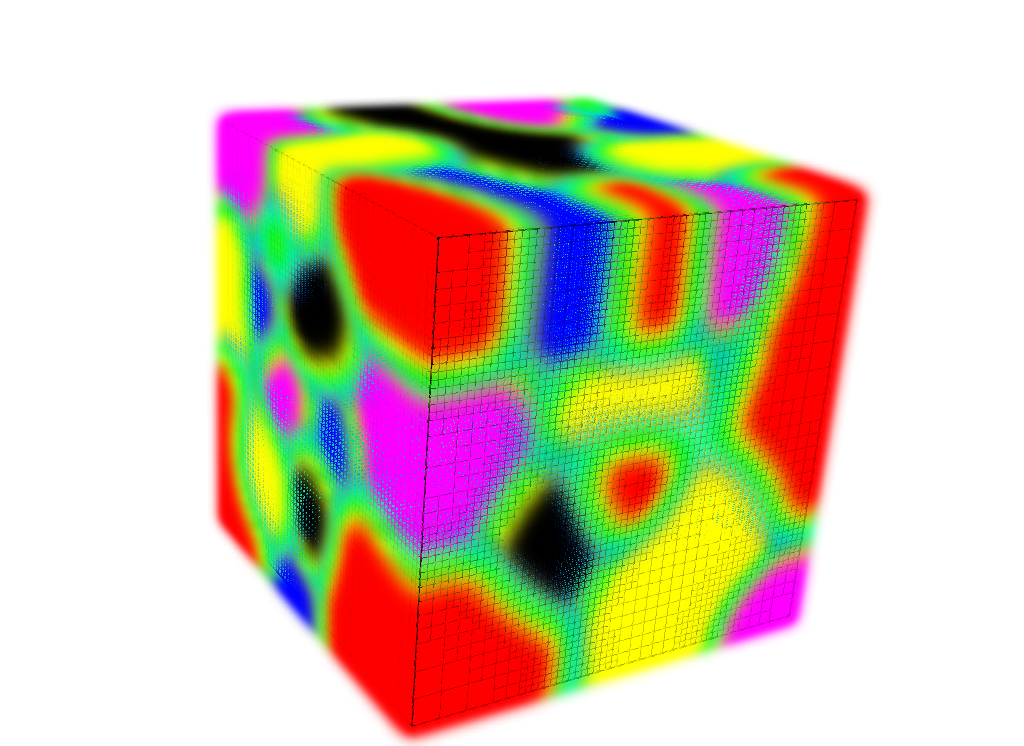
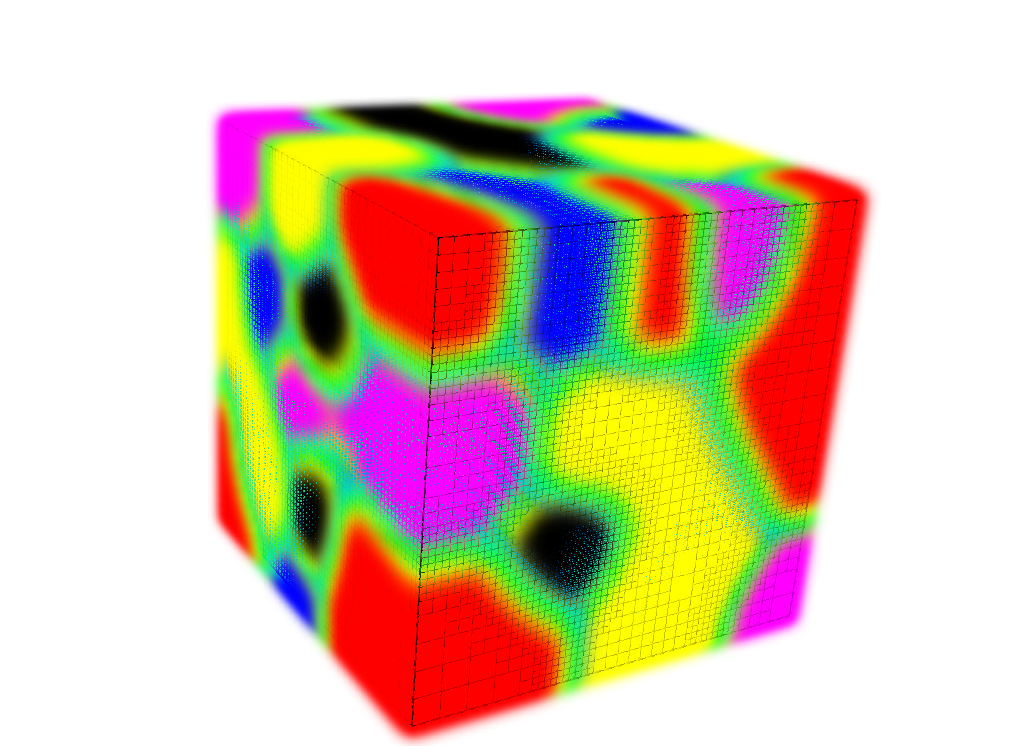
In combination with an adaptive mesh refinement approach, we were able to perform three-dimensional experiments in an efficient way. This project was in collaboration with Martin Stoll and partly with Peter Benner.
Image inpainting
Modified versions of the Cahn-Hilliard equation can be used for the solution of problems in image inpainting. Inpainting is the art of modifying parts of an image such that the resulting changes are not easily detectable by an ordinary observer. Applications include the restoration of damaged paintings and photographs, the replacement of selected objects, or the reduction of artifacts in medical images.
Cahn-Hilliard inpainting was proposed by Bertozzi et al. and is based on the two-component Cahn-Hilliard equation equipped with a smooth potential. We extended this approach in two ways: First, we applied a nonsmooth potential, which results in the solution of variational inequalities. The numerical results showed an increase of the color intensity when the nonsmooth potential is used. Second, we generalized the black-and-white Cahn-Hilliard inpainting model to gray value images. This new model is based on the multi-component Cahn-Hilliard equation. We studied efficient numerical solution techniques for the scalar and in particular for the vector-valued modified Cahn-Hilliard equation using the techniques developed in the above project. An important difference to the above project is that the modified Cahn-Hillard equation as a whole is not given by a gradient flow. Especially, the model arised as a superposition of two gradient flows. We applied the convexity splitting technique, which yields under the right conditions an unconditional gradient stable time-discrete scheme. Again, the core of our approach was the development of efficient practical preconditioners for the iterative solution of the large and sparse linear systems that arise from classical finite element methods. This project was in collaboration with Martin Stoll as well as partly with David Kay and Andy Wathen.