Caustic of light falling through a lens (Edmund Optics article #NT49-291)
where image formation is dominated by ray optics. For each wavelength, we
determine a polynomial system of degree 3, mapping light rays falling through
the entrance pupil to a location in the image plane. Left side: Jacobian of the mapping (crossed lines) and the filter derived
from it (Gaussian blobs). Right side: dense rendering. Analytical
derivatives are useful in various stages of a rendering pipeline.
Abstract
Simulation of light transport through lens systems plays an important role in graphics. While basic imaging properties can be conveniently derived from linear models (like ABCD matrices), these approximations fail to describe nonlinear effects and aberrations that arise in real optics. Such effects can be computed by proper ray tracing, for which, however, finding suitable sampling and filtering strategies is often not a trivial task. Inspired by aberration theory, which describes the deviation from the linear ray transfer in terms of wavefront distortions, we propose a ray-space formulation for nonlinear effects. In particular, we approximate the analytical solution to the ray tracing problem by means of a Taylor expansion in the ray parameters. This representation enables a construction-kit approach to complex optical systems in the spirit of matrix optics. It is also very simple to evaluate, which allows for efficient execution on CPU and GPU alike, including the computation of mixed derivatives of any order. We evaluate fidelity and performance of our polynomial model, and show applications in high-quality offline rendering and at interactive frame rates.Full Paper
| EGSR 2012 Paper (27MB) | [PolynomialOptics-Hullin2012.pdf] |
| Supplemental Document (166KB) | [PolynomialOptics-Supp-Hullin2012.pdf] |
Citation
@article{PolynomialOptics-Hullin2012,
author = {Matthias B. Hullin and Johannes Hanika and Wolfgang Heidrich},
title = {{Polynomial Optics}: A Construction Kit for Efficient Ray-Tracing of Lens Systems},
journal = {Computer Graphics Forum (Proceedings of EGSR 2012)},
volume = {31},
number = {4},
year = {2012},
month = jul,
}
|
Results
C
B
D
A
A HDR photo of a city at night (A) is imaged through a
virtual achromatic doublet (Edmund Optics #NT32-921), adding aberrations as
the aperture size is increased (B,
C). Note the subtle color variation within
each pattern, originating from the spectral dispersion of the optical
system. Deliberate defocus turns the point lights into fascinating patterns
(D). Data and source code
for this
figure are provided below.



Flare renderings of three different lens systems
generated using polynomial optics. From left to right: “canon” (34 optical
surfaces), “itoh” (19 surfaces) and “canon-anamorphic” (42 surfaces). Only indirect light was rendered, and
we used the incorrect assumption that all surfaces reflect the
same amount of light.
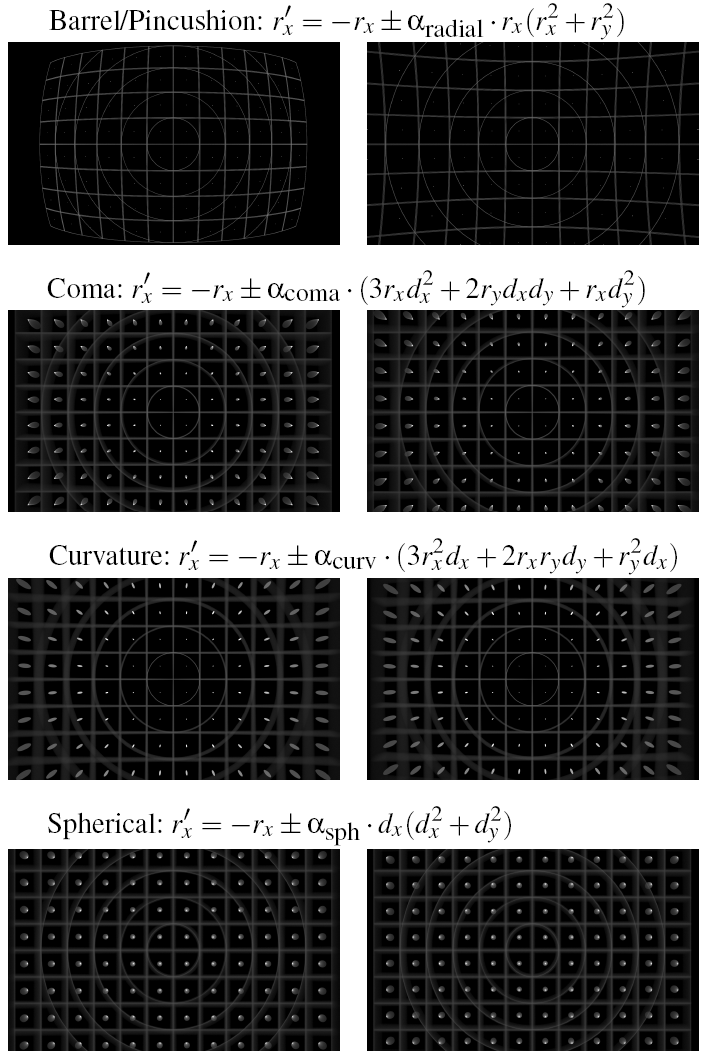
In a degree-3 polynomial produced by an axially
symmetrical lens system, we identify four groups of cubic
terms that form radially symmetric image distortions.
We provide the formula that maps the ray coordinate tuple
(rx;ry;dx;dy) to the image plane position r'x. Note that
Seidel’s aberration definitions (spherical aberration, coma,
field curvature, defocus) do not map exactly to our polynomial
basis; however, these phenomena do not occur in isolated
form in real optics either.
Source Code
Here we provide the source to our library under a BSD-like license: Feel free to do what you want with this code, as long as the copyright information from the file header remains intact. Needless to say, we appreciate proper attribution of our work, be it through citation of our paper, movie credits, or otherwise.| C++ code with examples (14 MB) | [PolynomialOptics-Source.zip] |
| "Light" package (no image included) (374KB) | [PolynomialOptics-Source-light.zip] |
| HDR input image for Postprocess Example (15MB) | [night2.pfm] |
| Readme file (4KB) | [README] |