Cutset UGM Demo

The previous demos considered acyclic models, but in many cases our model may have loops. Unfortunately, decoding/inference/sampling in general UGMs containing loops is NP-hard. Neverthess, in many cases we can take advantage of the graph structure to still yield an efficient polynomial-time algorithm. In this demo we consider the case of graphs that have a small cutset, which allows exact decoding/inference/sampling by using cutest conditioning.

Bus Queue Problem

The UBC campus shuttle is convenient for getting around campus quickly, but it only comes every 30 minutes and it has a limited capacity. Since we could walk anywhere on the route in less than 30 minutes, it is important to consider whether the bus will be full before we decide to walk to a bus stop. We might also want to think about the following conditional query: Given the number of people at a particular bus stop, how many people are likely to be at the previous bus stops (ie. will there be room on the bus by the time it gets to us)?

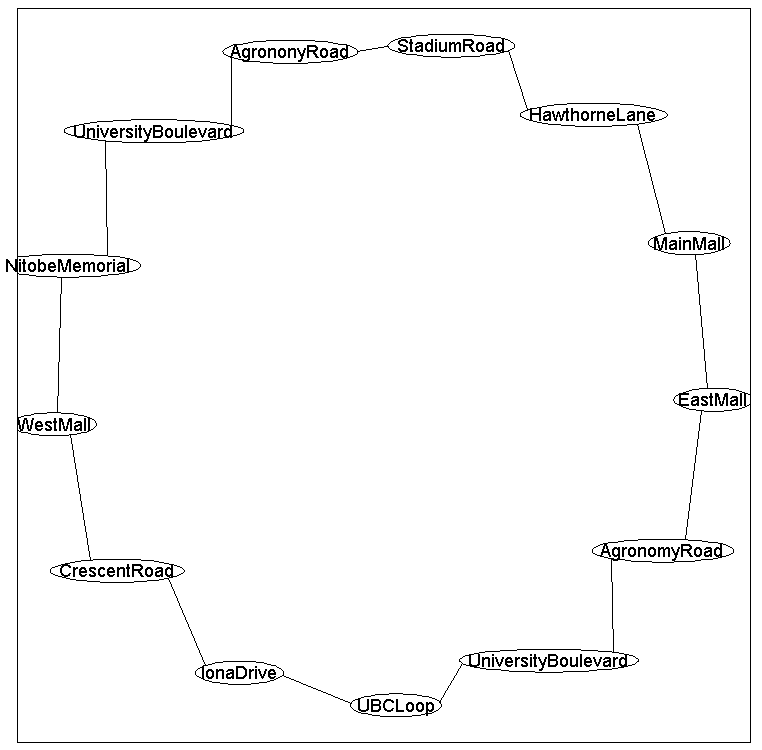
The bus makes 13 stops, and we will assume that at each stop we might have between 0 and 24 people (the maximum capacity of the bus) waiting at it. Since the bus route forms a loop and their exists a dependency between the number of people waiting at adjacent stops, we will use the following loop-structured graph:

Based on a rough empirical estimate, we will assume that the highest values of the node potentials for each of the stops is:

StopHighest nodePot
UBCLoop10
UniversityBoulevard8
AgronomyRoad0
EastMall3
MainMall5
HawthorneLane4
StadiumRoad0
AgrononyRoad5
UniversityBoulevard0
NitobeMemorial0
WestMall0
CrescentRoad0
IonaDrive0

We will assume that the node potentials decay according to a Gaussian around these modes.

To model correlations between adjacent stops, we will put the highest edge potential on adjacent stops having the same number of people. Subsequently, we will make the edge potentials decay according to a Gaussian based on the difference between the number of people at adjacent stops.

Representing the bus queue model with UGM

We first make the adjacency matrix and the edgeStruct: 
nNodes = 13;
nStates = 25;
adj = zeros(nNodes);
for i = 1:nNodes-1
    adj(i,i+1) = 1;
end
adj(nNodes,1) = 1;
adj = adj+adj';
edgeStruct = UGM_makeEdgeStruct(adj,nStates);
Now the node potentials: 
busy = [10
    8
    0
    3
    5
    4
    0
    5
    0
    0
    0
    0
    0];
nodePot = zeros(nNodes,nStates);
for n = 1:nNodes
   for s = 1:nStates
      nodePot(n,s) = exp(-(1/10)*(busy(n)-(s-1))^2);
   end
end
And finally the edge potentials: 
edgePot = zeros(nStates);
for s1 = 1:nStates
    for s2 = 1:nStates
        edgePot(s1,s2) = exp(-(1/100)*(s1-s2)^2);
    end
end
edgePot = repmat(edgePot,[1 1 edgeStruct.nEdges]);

Conditioning in the Bus Queue Problem

The high number of node/states in the model makes brute force decoding/inference/sampling intractable. Further, the presence of a loop means that our dynamic programming algorithms for tree-structured data will not work. Neverthess, it is still possible to do exact conditional decoding/inference/sampling in the model. This is because, as long we condition on at least one node, the loop will be broken in the conditional UGM. For example, if we condition on 'UBCLoop' then the conditional UGM has the following structure:

We recognize this as a chain structure, so we can use the methods discussed in previous sections for conditional decoding/inference/sampling. For example, if we want to do these conditional tasks given that 10 people are at the first stop, we use: 
clamped = zeros(nNodes,1);
clamped(1) = 11;

optimalDecoding = UGM_Decode_Conditional(nodePot,edgePot,edgeStruct,clamped,@UGM_Decode_Tree);
optimalNumber = optimalDecoding-1

optimalNumber =

    10
     8
     1
     3
     5
     4
     1
     4
     0
     0
     0
     0
     1

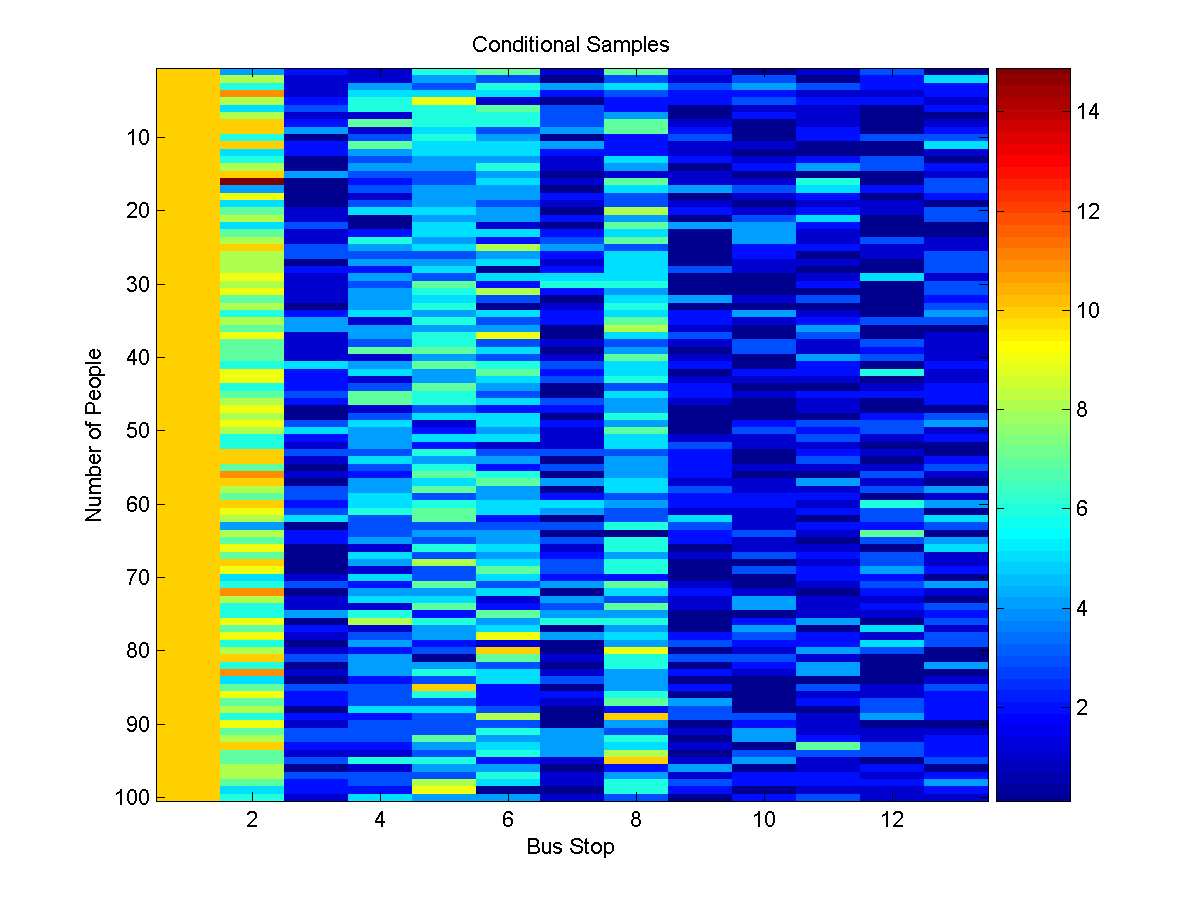
[nodeBel,edgeBel,logZ] = UGM_Infer_Conditional(nodePot,edgePot,edgeStruct,clamped,@UGM_Infer_Tree);

samples = UGM_Sample_Conditional(nodePot,edgePot,edgeStruct,clamped,@UGM_Sample_Tree);
figure(1);
imagesc(samples'-1);
xlabel('Bus Stop');
ylabel('Number of People');
title('Conditional Samples');
colorbar

Note that we used the tree functions above instead of the chain functions because the chain functions assume that the edges are organized in the proper order. However, the conditioning function in UGM is not guaranteed to place the edges in the conditional UGM in any particular order.

Cutset Conditioning for Joint Decoding/Inference/Sampling

Given that we can do conditional decoding for a fixed value of one of the nodes, it is a straightforward extension to find the optimal decoding. We just find the optimal conditional decoding for all 25 values of the first node (or some other node in the loop), compute the potential in the joint model for the first node's state and the optimal decoding given this choice, and take the maximum. This is an instance of a technique known as cutset conditioning, whose general form is roughly: Given that we can find the optimal decoding of a forest in O(nNodes*nStates^2), the runtime for the cutset conditioning algorithm for loop structures is O(nNodes*nStates^3), which is much faster than the exponential cost of examining all states.

We will use node 1 as the 'cutset', and use the cutset conditioning algorithm to find the optimal decoding: 

cutset = 1;
optimalDecoding = UGM_Decode_Cutset(nodePot,edgePot,edgeStruct,cutset)
optimalNumber2 = optimalDecoding-1;

optimalNumber =

     9
     8
     1
     3
     5
     4
     1
     4
     0
     0
     0
     0
     1
Cutset conditioning can also be used for computing the normalizing constant and marginals. To compute the normalizing constant, we simply add up the normalizing constants from the conditional UGMs (multiplied by the node and edge potentials that are missing from the conditional UGM) under each possible value(s) of the cutset variable(s). To compute marginals, we first compute conditional marginals under each assignment to the cutset variables, and then normalize the weighted sum of these marginals (where the weights come from the normalizing constants of the conditional UGMs, together with the node and edge potentials that are missing from the conditional UGM). This can be called with: 
[nodeBel,edgeBel,logZ] = UGM_Infer_Cutset(nodePot,edgePot,edgeStruct,cutset);
Sampling also works in an analogous way. We first compute the weights of the different possible values of the cutset variables. Then we generate a random value from the normalized distribution of the weights. This value is then used to generate a sample of the remaining variables given the corresponding value of the cutset variable. This can be called with: 
samples = UGM_Sample_Cutset(nodePot,edgePot,edgeStruct,cutset);
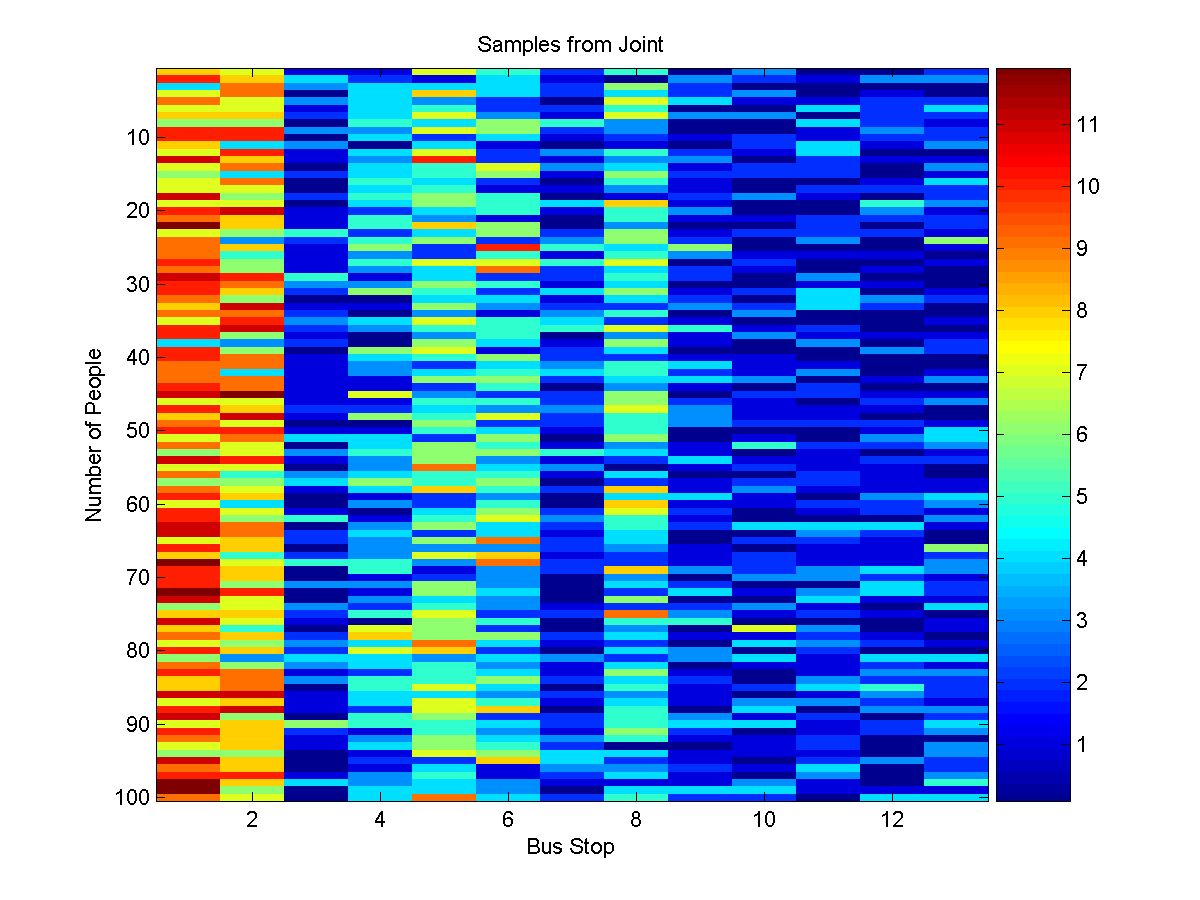
figure(2);
imagesc(samples'-1);
xlabel('Bus Stop');
ylabel('Number of People');
title('Samples from Joint');
colorbar

Extended Bus Queue Problem

In general, the UGM resulting from conditioning on a single variable might still have loops. Nevertheless, we can apply cutset conditioning for exact inference in general loopy UGMs if we allow the cutset to consist of more than one variable.

For example, consider a transit system with the following topological structure:

In this graph, there is no single node that we can condition on to make the conditional graph structure a forest. This is because no single node can break all of the loops present in the graph. However, if we simultaneously condition on all three nodes labeled 'Hub', then the conditional UGM is a set of independent chains. So, we can perform exact decoding/inference/sampling with a cutset conditioning algorithm where we loop over all possible values of these 3 cutset nodes. In this graph, the 'Hub' variables are nodes 1;70;81, so we can perform exact decoding/inference/sampling using: 

cutset = [1 70 81];
optimalDecoding = UGM_Decode_Cutset(nodePot,edgePot,edgeStruct,cutset);
[nodeBel,edgeBel,logZ] = UGM_Infer_Cutset(nodePot,edgePot,edgeStruct,cutset);
samples = UGM_Sample_Cutset(nodePot,edgePot,edgeStruct,cutset);
Although it is efficient if the size of the cutset is small, in general the runtime of cutset conditioning algorithms is exponential in the number of nodes in the cutset (as well as the number of states). For example, if we want to do decoding and the cutset needed to make the conditional UGM a forest has k elements, we will need to do decoding in s^k forests (where s is the number of states). Thus, cutset conditioning is only practical when the graph structure allows us to find a small cutset.

Notes

A reference describing cutset conditioning is: In some cases, the Markov independence properties between sets of cutset variables can be used to derive more efficient methods. However, this is not implemented in the current version of UGM. An alternative strategy for performing exact decoding/inference/sampling in loopy models is with junction trees, which are the subject of the next demo. Unfortunately, for general UGMs both cutset conditioning and junction tree methods require exponential time in the tree width of the graph.

In the model described above, the potentials on each edge form Toeplitz matrices. In a forest-structured UGM with Toeplitz edge potentials, it is possible to reduce the total computation time of the various belief propagation algorithms from O(nNodes * nStates^2) down to O(nNodes * nStates * log(nStates)), by taking advantage of techniques similar to the fast Fourier transform. This improvement allows us to use forest-structured models (or loopy models that admit a small cutset) where the number of states at each node is potentially enormous. More efficient versions of belief propagation are also possible if our edge potenttial matrices do not have Toeplitz structure but have a different type of structure that allows us to multiply by the edge potential matrix in less than O(nStates^2). However, these types of speed-ups are not implemented in the current version of UGM.

PREVIOUS DEMO NEXT DEMO

Mark Schmidt > Software > UGM > Cutset Demo