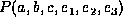Consider the Bayesian network in Figure 1.
It factorizes the joint probability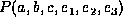 
into the following list of factors:
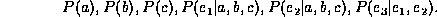
We say that this factorization is homogeneous because all the factors are combined in the same way, i.e., by multiplication.
Now suppose the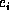 
's are convergent variables. Then their
conditional probabilities can be further factorized as
follows:
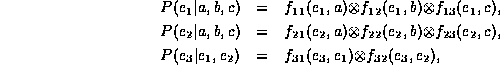
where the factor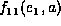 
, for instance, is the contributing factor
of a to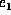 
.
We say that the following list of factors
constitute a
heterogeneous factorization of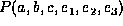 
because the joint probability can be obtained by combining those factors
in a proper order using
either multiplication or the operator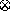 
.
The word heterogeneous is to signify the fact that
different factor pairs might be combined in different ways.
We call each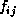 
a heterogeneous
factor because it needs to be combined with the other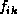 
's
by the operator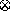 
before it can be combined
with other factors by multiplication. In contrast, we
call the factors 
, 
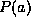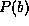, and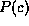 
homogeneous factors.
We shall refer to that heterogeneous factorization as the heterogeneous factorization represented by the BN in Figure 1. It is obvious that this heterogeneous factorization is of finer grain than the homogeneous factorization represented by the BN.
