

Go backward to 2 Adding to the Electrical Domain
Go up to Top
Go forward to 4 Designing Video Presentations
3 House Plumbing
Consider the domain of house plumbing represented in
the following diagram:
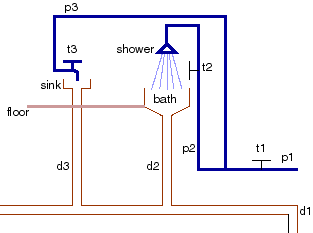
The Plumbing Domain
In this example constants p1, p2 and p3 denote cold water
pipes. Constants t1, t2 and t3 denote taps and d1, d2 and
d3 denote drainage pipes. The constants shower denotes a shower,
bath denotes a bath, sink denotes a sink and floor denotes the
floor.
The diagram above
is intended to give the denotation
for the symbols.
Suppose we have as predicate symbols:
- pressurised, where pressurised(P) is true if pipe P has
mains pressure in it.
- on, where on(T) is true if tap T is on.
- off, where off(T) is true if tap T is off.
- wet, where wet(B) is true if B is wet.
- flow, where flow(P) is true if water is flowing through P.
- plugged, where plugged(S) is true if S is either a sink or
a bath and has the plug in.
- unplugged, where unplugged(S) is true if S is either a sink or
a bath and has the plug in.
The file plumbing.pl
contains a CILog axiomatization for how water can flow down drain d1 if
taps t1 and t2 are on and the bath is unplugged.
- Finish the axiomatization for the sink in the same manner as the
axiomatization for the bath. Test it in CILog.
- Axiomatize how the floor is wet if the sink overflows or the
bath overflows. They overflow if the plug is in and water is flowing
in. You may invent new predicates as long as you give their intended
interpretation. [Assume that the taps and plugs have been in the same
positions for one hour; you don't need to axiomatize the dynamics of
the turning on taps and inserting and removing plugs.] Test it in
CILog.
- Suppose there is a hot water system is installed to the left of
tap t1. This has another tap in the pipe leading into it, and
supplies hot water to the shower and the sink (there are separate hot
and cold water taps for each). Add this to your axiomatization. Give
the denotation for all constants and predicate symbols you
invent. Test it in CILog.
You need to hand in a complete listing of your program, including the
intended interpretation for all symbols used and a trace of the CILog
session to show it runs.
Computational
Intelligence online
material, ©David Poole, Alan Mackworth and Randy Goebel, 1999