Abstract
Multiplexing is a common technique for encoding high-dimensional image data into a single, two-dimensional image. Examples of spatial multiplexing include Bayer patterns to capture color channels, and integral images to encode light fields. In the Fourier domain, optical heterodyning has been used to acquire light fields.In this paper, we develop a general theory of multiplexing the dimensions of the plenoptic function onto an image sensor. Our theory enables a principled comparison of plenoptic multiplexing schemes, including noise analysis, as well as the development of a generic reconstruction algorithm. The framework also aides in the identification and optimization of novel multiplexed imaging applications.
Overview
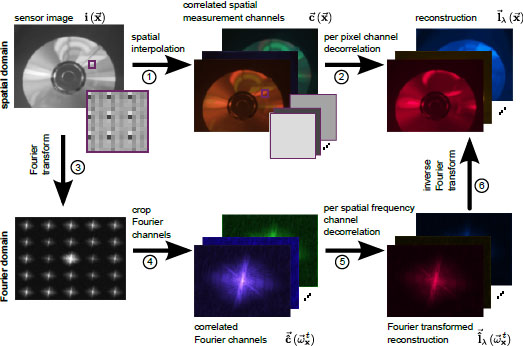 |
|
Overview of multiplexed image reconstruction. The
plenoptic function can be reconstructed by interpolating all measurement
channels and performing a local decorrelation in the spatial
domain (upper row). Alternatively, it can be reconstructed
in the Fourier domain by cropping and locally decorrelating the
Fourier channels created by the plenoptic modulator (lower row). This schematic illustrates our mathematical
framework that unifies many previously proposed multiplexing and corresponding reconstruction approaches. |
Case Studies
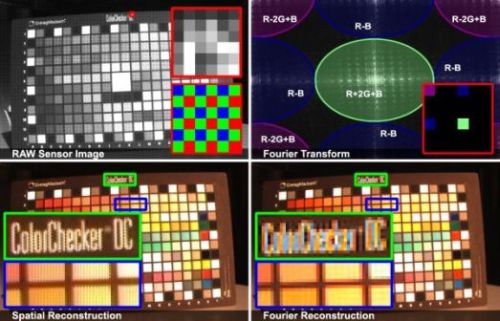 |
|
Multiplexing Color Information. Raw sensor image with magnified part and corresponding
CFA (upper left). Fourier transform with channel correlations illustrated for the entire image and the magnified CFA (upper
right). Reconstruction of the non-perfectly bandlimited signal in the spatial (lower left) and Fourier (lower right) domain reveal different
aliasing artifacts. |
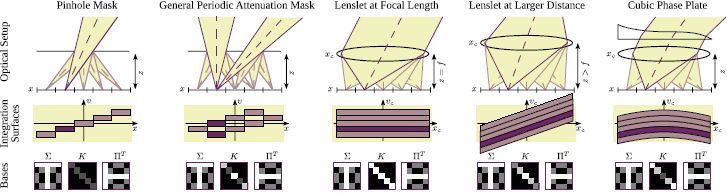 |
|
Our theory applied to light field imaging.
Columns 1 to 5 illustrate different light field
camera configurations (upper row), corresponding integration surfaces in light field space for the individual sensor pixels (center row), and
the spatial and plenoptic basis functions (lower row). The convolution of a periodic attenuation mask can be separated into a spatial and plenoptic
part using the Fourier basis (column 2). Integration surfaces for refractive optical elements already include the mapping g^-1 from
sensor space to camera or world space on the microlens plane. |
 |
|
Comparison of reconstruction quality for Cones data set (Veeraraghavan et al. [2007]).
All results are three-times upsampled during reconstruction.
Left: upsampling by zero-padding the 4D inverse FFT. Center: low resolution 4D inverse FFT followed
by bicubic upsampling. Right: bicubic up-sampling of correlated measurement channels followed by local decorrelation. |
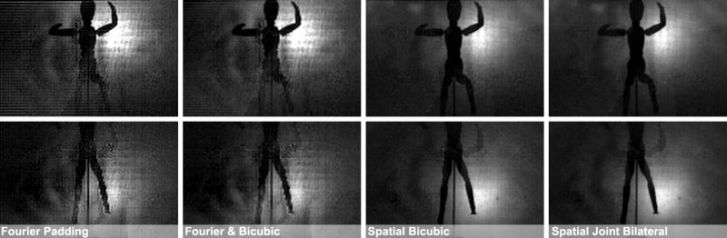 |
|
Comparison of reconstruction quality for Mannequin data set (Lanman et al. [2008]).
The results are three-times upsampled and show two different views of the reconstruction, one in each row.
First column: upsampling by zero-padding the 4D inverse FFT. Second column: low resolution 4D inverse FFT followed
by bicubic upsampling. Third column: bicubic up-sampling of correlated measurement channels followed by local decorrelation.
The right-most column shows an example that was computed with a non-linear spatial filter - the joint bilateral filter. |
 |
|
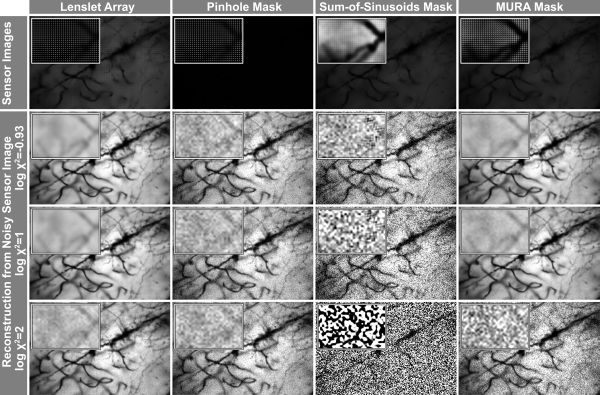
Comparison of noise amplification for different light field acquisition schemes on the golgi stained neuron dataset (lightfield.
stanford.edu). The upper row shows simulated sensor images with contrast enhanced close-ups. The other rows show a single
view of the reconstructed light field from a noisy sensor image. The ratio chi^2 of signal-dependent photon noise and signal independent dark
current noise varies for the different reconstructions. Row 2 simulates a reconstruction with a dominating additive noise term, while rows
3 and 4 show the effect of an increasingly dominating photon noise term in the sensor images. |
Files
| IJCV 2012 Paper | [pdf] [bib] |
| CVPR 2010 Paper | [pdf] [bib] |
| CVPR 2010 Supplemental material | [pdf] |
| Video | [mov] |
| Code and datasets | [tgz] |
Related Projects
State of the Art in Computational Plenoptic ImagingSensor Saturation in Fourier Multiplexed Imaging