A mask-modulated LDR image captured with our prototype scan camera (a). The pattern introduced by the mask and saturated
regions are enlarged on the upper left. The Fourier transform of the captured image (b) contains nine copies, of which three (b, top) are
individually transformed into the spatial domain and reveal saturation artifacts (see below for enlargement). The tone-mapped result of
our reconstruction (c) does not contain the mask pattern or Fourier copies. The right part shows a linearly mapped exposure sequence of
an unmodulated LDR image (d) and our reconstruction (e) compared to ground truth images (f).Abstract
Optically multiplexed image acquisition techniques have become increasingly popular for encoding different exposures, color channels, light-fields, and other properties of light onto two-dimensional image sensors. Recently, Fourier-based multiplexing and reconstruction approaches have been introduced in order to achieve a superior light transmission of the employed modulators and better signal-to-noise characteristics of the reconstructed data.We show in this paper that Fourier-based reconstruction approaches suffer from severe artifacts in the case of sensor saturation, i.e. when the dynamic range of the scene exceeds the capabilities of the image sensor. We analyze the problem, and propose a novel combined optical light modulation and computational reconstruction method that not only suppresses such artifacts, but also allows us to recover a wider dynamic range than existing image-space multiplexing approaches.
Overview
 |
Fourier Multiplexed Imaging. A simulated, band-limited optical signal is filtered with
a semi-transparent mask. According to the convolution theorem,
this multiplication corresponds to a convolution in the frequency
domain. Fourier multiplexing approaches exploit the resulting
copy mechanism to capture several differently filtered versions of
a scene in different frequency bands of a photograph. |
 |
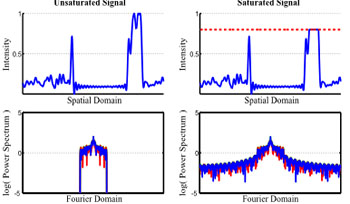Artifacts from Partial Saturation. A band-limited signal (upper left), consisting of a single
scanline taken from a high dynamic range image, and the same
signal clipped at 0.8 maximum intensity level (upper right). The
Fourier transform of the original scanline is band-limited (lower
left), while the Fourier transform of the clipped version of the same
scanline is corrupted by high frequency components. |
 |
Artifacts from Full Saturation. A constant signal captured through a 3x3 pattern of
neutral density filters and its Fourier transform (left pair). Partial saturation of this sensor image causes changes in the magnitudes
of the signal`s Fourier copies (right pair). Peak magnitudes are color-coded. |
 |
Sensor saturation yields ringing and other artifacts in Fourier multiplexed data. This image is the spatial version of one of the higher frequency tiles in the teaser above. |
Results
 |
| Our prototype is a large format high-resolution scanner camera. The filters are mounted under a diffuser on the scanner`s glass plate. |
 |
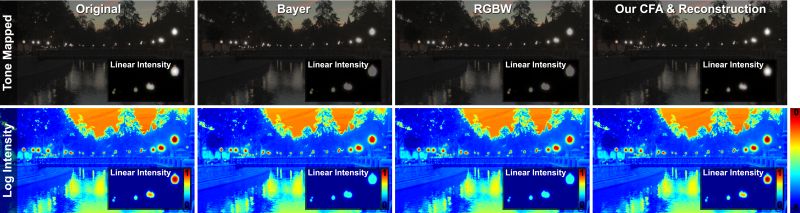| A comparison of color imaging through a standard Bayer color filter array (center left column), an RGBW CFA with the same light transmission (center right column), and our CFA with the proposed reconstruction (right column). A sensor image was simulated for all three cases with a dynamic range of 4% of that of the photographed scene. The upper row shows the tone mapped original image and the three reconstructions with linearized magnifications. The lower row shows color coded logarithmic intensities and linear intensities in the magnifications. |
 |
|
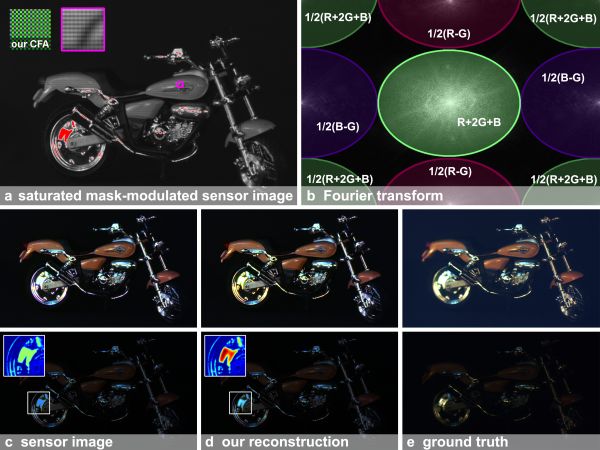
A sensor image captured with our prototype through
a novel CFA with saturated regions in red (a). The mask creates
two differently scaled luma and two chroma copies in the Fourier
transform (b). The dynamic range of the captured image can be
significantly extended using our optimization approach as seen in
the recolored magnifications in the lower images. |
Files
| Erratum | Equation 5 is incorrect in the paper. Please find the derivation here. |
| Paper | [pdf] [bib] |
| Video | [mov] |
Related Projects
A Theory of Plenoptic MultiplexingState of the Art in Computational Plenoptic Imaging