|
International
Journal of Shape Modeling – Special Issue on SMI’06 - June 2007
Download:
IJSM paper (b/w) ,
SMI paper (color),
Presentation slides (color),
SIGGRAPH poster
(ppt) ,
(pdf)
,
Bibtex:
@ARTICLE{Popa:2007,
author = { Tiberiu Popa and Dan Julius and Alla Sheffer},
title = { Interactive and Linear Material Aware
Deformations},
journal = {International Journal of Shape modeling},
year = {2007},
}
Abstract
Most real world objects consist of non-uniform
materials; as a result, during deformation the bending and shearing are
distributed non-uniformly and depend on the local stiffness of the
material. In the virtual environment there are three prevalent approaches
to model deformation: purely geometric, physically driven, and skeleton
based. This paper proposes a new approach to model deformation that
incorporates nonuniform materials into the geometric deformation framework.
Our approach provides a simple and intuitive method to control the distribution
of the bending and shearing throughout the model according to the local
material stiffness. It also provides a rich, flexible and intuitive user
interface. Thus, we are able to generate realistic looking, material-aware
deformations at interactive rates. Our method works on all types of models,
including models with continuous stiffness gradation and non-articulated
models such as cloth. The material stiffness across the surface can be
specified by the user with an intuitive paint-like interface or it can be
learned from a sequence of sample deformations.
|
 . .
|
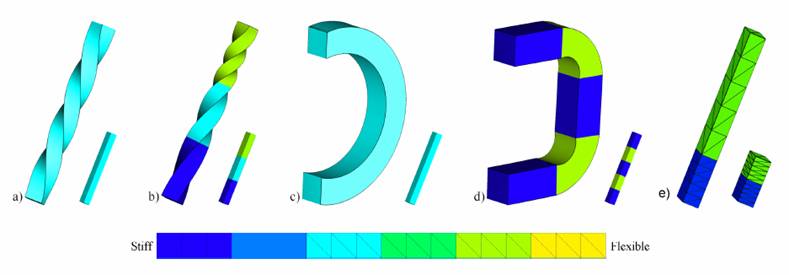
Overview
|
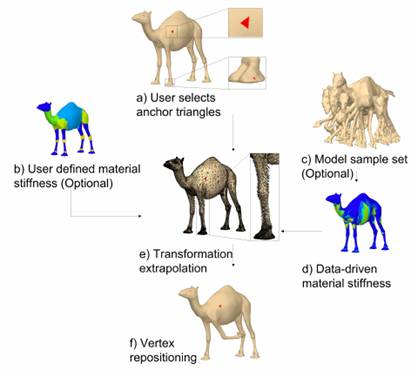
Input:
a) User selects a small set of triangles, called anchor
triangles (Figure 3(a)) and apply the desired transformations using a click
and drag motion. We support anchor transformations that include any
combination of rotations and uniform scales.
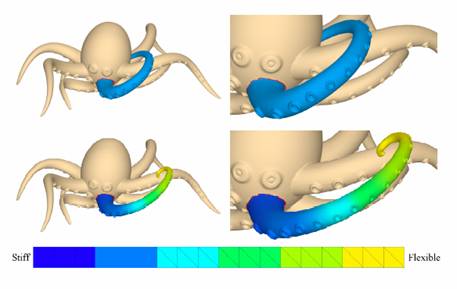
b) User defines the stiffness of the material using a
simple and intuitive paint-like interface. The method also supports
continuous variation of stiffness such as stiffness gradient as the
tentacle’s octopus from the above figure.
c, d) The material stiffness can also be computed
automatically from a set of sample poses.
Output:
e) From the anchor triangles, we then propagate
transformations to the remaining triangles of the mesh consistent to the
material properties
f) We glue the triangles together for a manifold final
result
|
 . .
|
Direct Vertex Manipulation
|
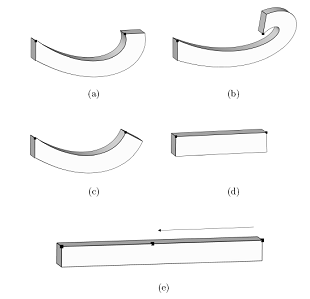
In certain cases the user might want to specify positional
constraints as well. We developed a method where the user specifies positional
constraints on vertices by dragging them on the screen and the system then
computes optimal rotations automatically. Figure 5 shows an example where a
straight bar (5e) is deformed by dragging one of its vertices. Depending on
the energy functional used, our system can simulate various behaviours:
a) Area
b) Volume
c) Shear
d) Dihedral
angles (in the L2 norm)
|
.
|
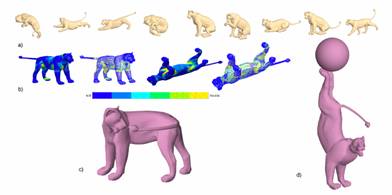
Material Learning
|
In many situations, physically or anatomically correct
deformation samples of a given model may already be available. In such
cases we would like to derive the material properties from the sample poses
to create new deformations which are consistent with the sample set and are
therefore also correct.
a) A
set of sample lion poses
b) Derived
material properties
c) New
deformations
|
.
|
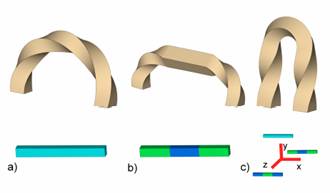
Anisotropic Materials
|
The formulation presented so far assumes that bending flexibility
is a non-directional property, which need not be true in practice. For
example, a knee joint is only flexible in one direction and rigid in the
other two. We extend our formulation to allow different bending stiffness for
different axes of rotation.
This figure sows the result of bending and twisting a
bar under:
a) Isotropic
uniform material
b) Isotropic
non-uniform material (middle section is isotropically stiffer than the rest
of the bar)
c) Anisotropic
non-uniform material (middle section is stiffer under twisting and more
flexible under bending than the rest of the bar)
|
.
|
|