Understanding the Evolution of Linear Regions in Deep Reinforcement Learning
SETAREH COHAN, The University of British Columbia, Canada NAM HEE KIM, Aalto University, Finland DAVID ROLNICK, McGill University, Canada MICHIEL VAN DE PANNE, The University of British Columbia, Canada

Policies produced by deep reinforcement learning are typically characterised by their learning curves, but they remain poorly understood in many other respects. ReLU-based policies result in a partitioning of the input space into piecewise linear regions. We seek to understand how observed region counts and their densities evolve during deep reinforcement learning using empirical results that span a range of continuous control tasks and policy network dimensions. Intuitively, we may expect that during training, the region density increases in the areas that are frequently visited by the policy, thereby affording fine-grained control. We use recent theoretical and empirical results for the linear regions induced by neural networks in supervised learning settings for grounding and comparison of our results. Empirically, we find that the region density increases only moderately throughout training, as measured along fixed trajectories coming from the final policy. However, the trajectories themselves also increase in length during training, and thus the region densities decrease as seen from the perspective of the current trajectory. Our findings suggest that the complexity of deep reinforcement learning policies does not principally emerge from a significant growth in the complexity of functions observed on-and-around trajectories of the policy.
Summary
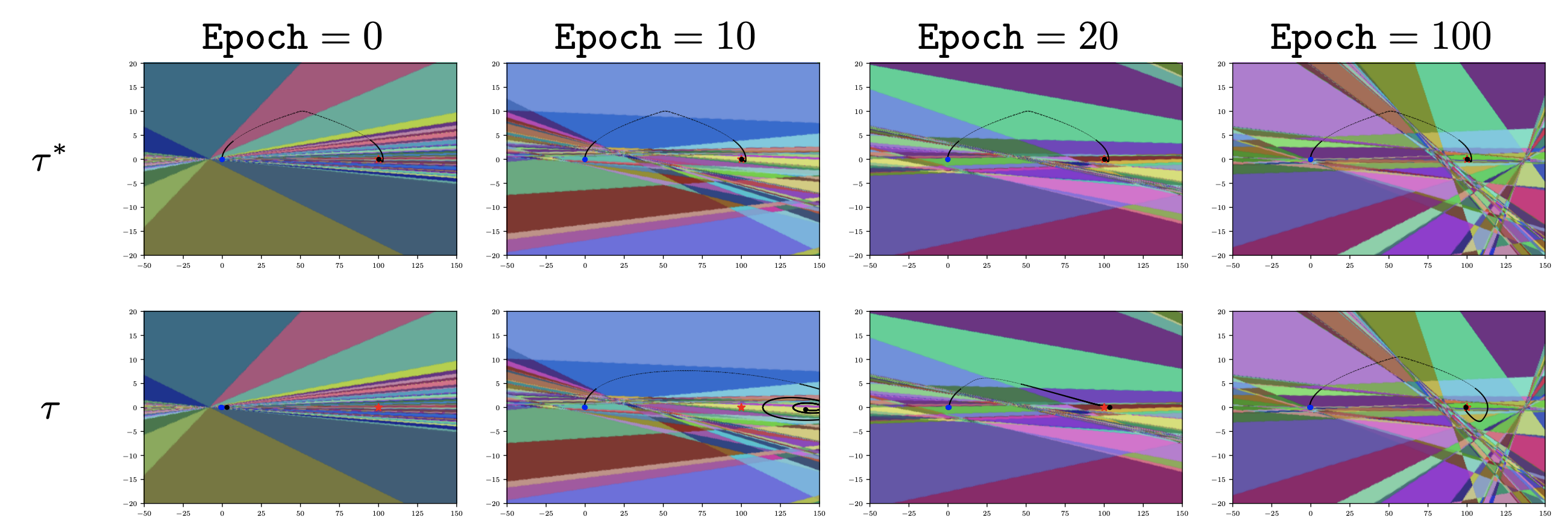
Our approach in investigating the evolution of linear regions of ReLU-based deep RL policies, lies in studying how the local granularity of linear regions evolve during training as measured along trajectories sampled from the policy. To compute the density of linear regions over episodic trajectories, we sweep the state space over the the corresponding trajectory. For each input state of the trajectory, we encode neurons of the policy network with a binary code 0 if the pre-activation is negatie, and with a 1 otherwise. The linear region of the input can thus be uniquely identified by the concatenation of these binary codes called an activation pattern. We are intested in the number of transitions in activation patters, as we sweep along trajectories.
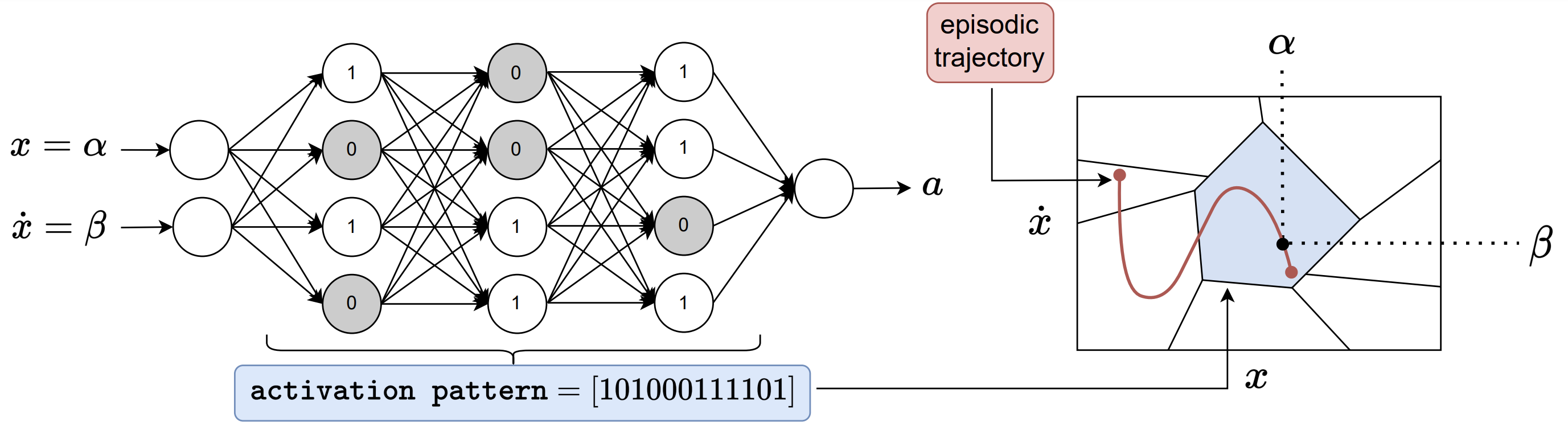
Metrics
For each trajectory, we compute three metrics: 1) the total number of region transitions over the trajectory, 2) the number of unique visited regions over the trajectory, and 3) the density of regions computed by dividing the number of region transitions by the length of the trajectory.
Trajectoies
We consider two types of trajectories: 1) fixed trajectories sampled from the final fully trained policy, and 2) current trajecotries sampled from the current snapshot of the policy during training.
Citation
@inproceedings{cohan2022understanding,
author = {Cohan, Setareh and Kim, Nam Hee and Rolnick, David and van de Panne, Michiel},
booktitle = {Advances in Neural Information Processing Systems},
title = {Understanding the Evolution of Linear Regions in Deep Reinforcement Learning},
url = {https://arxiv.org/pdf/2210.13611v2.pdf},
year = {2022}
}