Conditional UGMs

Consider the following simple pairwise UGM.

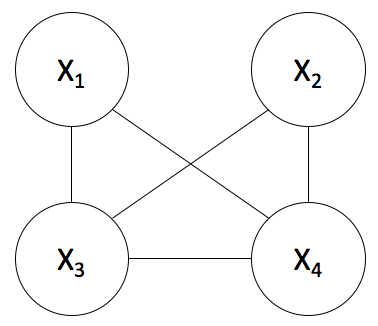
From the general formula for pairwise UGMs given in class, we have that: $$ p(x_1, x_2, x_3, x_4) = \frac{1}{Z}\prod_{j=1}^4 \phi_j(x_j)\prod_{\{i,j\} \in E} \phi_{i,j}(x_i,x_j) $$

To see what happens when we condition on variables, let's write this formula out explicitly for the simple UGM shown above.

$$ p(x_1, x_2, x_3, x_4) = \frac{1}{Z}\phi_1(x_1)\phi_2(x_2)\phi_3(x_3)\phi_4(x_4) \phi_{1,3}(x_1,x_3)\phi_{1,4}(x_1,x_4)\phi_{2,4}(x_2,x_4)\phi_{3,4}(x_3,x_4)\phi_{2,3}(x_2,x_3) $$

Now, in general, to get a particular marginal (e.g. $p(x_1)$) we have to sum over all the values the other random variables ($x_2, x_3, x_4$) can take on. I.e. $$ p(x_1) = \sum_{x_2\in {X_2}}\sum_{x_3\in {X_3}}\sum_{x_4\in {X_4}}p(x_1, X_2 = x_2, X_3=x_3, X_4=x_4) $$

This is computationally hard in general - but can be much easier if we get to condition on variables that make our UGM simplier. To see how the conditional UGM may be simplier than the full UGM, let's let $x_3 = a$ and $x_4 = b$ (where $a$ and $b$ are some values in the support of $x_3$ and $x_4$ respectively) and see what the resulting conditional distribution looks like:

$$ p(x_1, x_2| x_3=a, x_4=b) = \frac{1}{Z}\phi_1(x_1)\phi_2(x_2)\phi_3(a)\phi_4(b) \phi_{1,3}(x_1,a)\phi_{1,4}(x_1,b)\phi_{2,4}(x_2,b)\phi_{3,4}(a,b)\phi_{2,3}(x_2,b) $$

Now, notice that $\phi_3(a), \phi_4(b)$ and $\phi_{3,4}(a,b)$ are just some constants which we could push into our normalizing constant $Z$ and $\phi_{1,3}(x_1,a), \phi_{2,4}(x_2,b) $ and $\phi_{2,3}(x_2,b)$ are now just functions of $x_1$ and $x_2$ respectively. So we could rewrite our conditional distribution more simply as: $$ p(x_1, x_2| x_3=a, x_4=b) = \frac{1}{Z'}\phi'_1(x_1)\phi'_2(x_2) $$ where $\phi'_{1}(x_1) = \phi_{1}(x_1)\phi_{1,3}(x_1,a)\phi_{1,4}(x_1,b)$ and simmilarly for $\phi'_{2}(x_2)$ and the new normalizing constant $Z'$ ensures everything sums to one. This formula is equivalent to an even simpler UGM where computing the marginals is trivial,

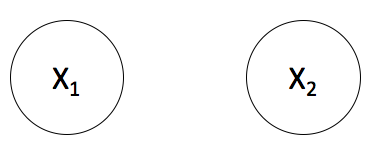
In question 1 you have to do this in a more complex UGM (you don't have to go through this tedious derivation - that was just for your understanding), but the procedure is the same - figure out what the conditional UGM looks like and then use what you know about the computational complexity of computing marginals for the conditional UGM to answer the question.

Bayesian Inference

The conjugate priors question uses similar mechanical steps to those you've used in the past so we just looked at how you'd get started with each question and left the mechanics for you to figure out.

1. You have the likelihood $p(y | \theta, \alpha)$ and the prior $p(\theta | \alpha)$, so you can just use Bayes rule to get the posterior: $p(\theta | y, \alpha) = \frac{1}{Z}p(y | \theta, \alpha)p(\theta | \alpha)$ and then substitute in the formulae for the prior and likelihood and solve for the resulting distribution.

2. You're given $p(y|\alpha) = \int p(y,\theta | \alpha) d\theta$. By the chain rule of probability $\int p(y,\theta | \alpha) d\theta = \int p(y |\theta , \alpha)p(\theta | \alpha) d\theta$ and you have expressions for both of those terms. From there you just have to manipulate the expression into the form of a distribution that you recognise to solve the integral.

Questions 3 and 4 follow similar steps.

Project advice

There was some discussion on where to get access to GPU resources. Obviously if you can borrow resources from someone who has a GPU that's ideal, but if you can't find anyone willing to share the GPUs, Amazon is a pretty cost effective alternative. I've used AWS spot instances for about $0.20 per an hour before - so 10 hours of GPU training cost less than the price of a cup of coffee. There are a lot of tutorials online for how to get set up so I won't repeat them here (also - Mike Gelbert is going through this in 340 on Monday)...

The only big gotcha to watch out for is that if you're using spot instances, they can die at any time (if the spot price goes above what you bid)... to avoid waisting work, I'd stongly advise you to save model checkpoints while you're training and then have a second script that's periodically backing up your work to somewhere safe.

We discussed going through an example of getting a GAN up and running in tensorflow and pytorch next week. If anyone has any other requests, send them through...