 plumbing2.gif
plumbing2.gif
CS502 Fall 2006
Assignment 3
Due: 12:30pm, Monday 16 October 2006.
p(X) <- q(X). p(Y) <- r(Y). q(a). r(b).Suppose there are two individuals fred and mary.
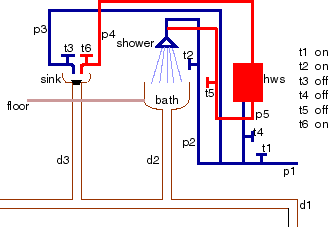
In this example, constants p1, p2 and p3 denote cold water pipes. p1 is the pipe coming in from the main water supply. Constants p4 and p5 represent hot water pipes (coming out from the hot water system). Constants t1, t2 t3, t4 and t5 denote taps and d1, d2 and d3 denote drainage pipes. The constants shower denotes a shower, bath denotes a bath, sink denotes a sink, hws denotes a hot water system, and floor denotes the floor. The diagram below is intended to give the denotation for the constant symbols.
 plumbing2.gif
plumbing2.gif
Suppose we have as predicate symbols:
The file plumbingbuggy.pl contains a CILog axiomatization for the case where tap t1 is on, t2 is on, t3 is off, t4 is off, t5 is off, and t6 is on. There is a plug in the sink, but not in the bath. (This has been formatted to be unreadable, but you don't need to be able to read the program, or know how it is implemented, to be able to debug it.)
Unfortunately there is a bug in the program. We know this because we can prove that the floor is wet, even though it isn't wet in the intended interpretation. Using CILog, your goal is to find a clause that is false in the intended interpretation, using just the intended interpretation of the symbols.
You need to hand in a trace of the CILog session, and show clearly which is the buggy rule.
Suppose there are three computers, named c1, c2 and c3, two rooms, r101 and r202, and three printers pr1, pr2 and pr3. Each computer has a room selected. Each room can have a printer plugged into its port.
Using CILog, we want to axiomatize a domain so that you can answer questions about which room a document was printed and which printer it was printed on.
Building, residential building, house, apartment building, condominium building, duplex, townhouse, owner-occupied, rental, multi-family dwelling, commercial building, mixed commercial-residential building.