Assignment One: Search
Due: 12:30pm, Monday 25 September 2006
http://www.cs.ubc.ca/labs/lci/CIspace/
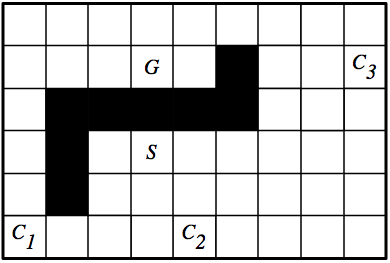
Consider the grid world in the following figure:
Assume that the robot can be in any of the white squares, and can do one
step up, down, left, or right at each time. It cannot step into one of
the black squares or outside of the boundary. The cost of a path is the number of
steps in the path. At the squares marked with
Ci are coffee shops where, if the robot goes to the square, it will
be given coffee. Suppose the robot starts at the square
marked as S, without coffee, and must end up at the square marked
G carrying coffee.
- What is the state space? How many states are there?
- Draw the graph that represents the search space. You can use
whatever notation you like as long as you explain it.
- Give an admissible heuristic. Your heuristic can take into
account where the coffee shops are, but not where the blocked squares
are. Hint: a useful concept is the Manhattan distance between two
points (x1,y1) and (x2,y2) which is |x1-x2|+|y1-y2|.
- On your graph number the nodes in the order they are expanded in
an A* search with multiple path pruning.
- How will your heuristic and A* change if we assume that there is a hill going
down towards the right so that
steps to the right cost 0.5 and steps to the left cost 1.5, and
steps up and down cost 1 each.
- The state space can be seen as a triple <x,y,c> where x is
the horizontal position, y is the vertical position and c is a
Boolean variable that specifies whether the robot has coffee. There
are 89 states (there are 46 squares the robot could be at with coffee
and 43 squares the robot could be without coffee).
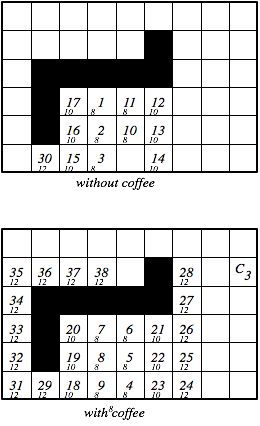
- A graph that represents the search space:
On the left is the states without coffee, and on the right are the
states with coffee. There is a state for each white square that is not
labeled with a Ci on the left graph, and a state for each white
square on the right graph. The neighbors of a node are the white
squares adjacent to it, except for the nodes that would lead to one of
the Ci squares in the left graph--these lead to the corresponding
Ci node on the right graph.
- An admissible heuristic. For a node <x,y,true> (i.e., a
state where the robot has coffee), h(<x,y,true>) is the
Manhattan distance from <x,y> to the location G. For a node <x,y,false> (i.e., a
state where the robot doesn't have coffee) h(<x,y,false>) is
the minimum (over i∈{1,2,3}) value of the Manhattan distance from <x,y> to
Ci plus the Manhattan distance from Ci to G. This would be
an exact distance, if not for the walls.
- Here are the states with the nodes in the order they are expanded in
an A* search with multiple path pruning. The number in the center
is the order the node is expanded. The number at the bottom is the
f-value of the node. This assumes that for the nodes with the same
f-value, the node added
last is expanded first.
Note that the path found goes straight down from S, then turns left
to C1 then up and right to G.
- How will your heuristic and A* change if we assume that there is a hill going
down towards the right so that
steps to the right cost 0.5 and steps to the left cost 1.5, and
steps up and down cost 1 each.
You can modify the Manhattan distance by seeing whether you go right
or left and use 1.5 for the cost when you have to go left and 0,5 when
it is right. A* search does not change as every node has the same
f-value (the costs and the h-values are different, but the
differences cancel out when summing).
Progress is made in science by observing a phenomenon of interest,
making hypotheses and testing the hypothesis either empirically or by
proving theorems.
For this question you are to think about the effect of heuristic
accuracy on A* search. That is, you are to experiment with, and
think about how close h(n) is to the actual distance from node n
to a goal affects the efficiency and accuracy of A*. To get full
marks you must at least invent and prove one theorem and show some
empirical evidence for you answer. Your answers need to be precise
(e.g, don't say "it works better", but say something like "it always works
better", "it sometimes works better" or "it works better in a
majority of cases").
- What is the effect of reducing h(n) when h(n) is already an
underestimate?
- How does A* perform when h(n) is the exact distance from
n to a goal?
- What happens if h(n) is not an underestimate?
One way to vary h(n) is to use the applet with the automatic
node heuristics (under the search options menu) turned on, then turn
it off and change heuristic values. There are ways to change all
heuristic values.
- What is the effect of reducing h(n) when h(n) is already an
underestimate?
At the top level of abstraction the answer is "more nodes are
expanded", however, it could be the case that the same number of
nodes are expanded. "no fewer nodes are expanded". However, if you
try this on lots of examples with multiple paths to the node you will
find this this
isn't true either! The reason is that a different optimal path may be
found. One true statement is that any sub-optimal path explored with
h1 will be
will be explored with h2 if h2(n) <= h1(n) <= cost(n,g),
where cost(n,g) is the actual cost from n to g.
- How does A* perform when h(n) is the exact distance from
n to a goal?
This depends on what happens when there are multiple optimal paths to
the goal. If the frontier acts as a stack for nodes with equal
f-values, then it will proceed to the goal without expanding any
node off a single optimal path.
- What happens if h(n) is not an underestimate?
It need not find an optimal path. However there are some general
statements that are true:
If h(n) <= cost(n,g)+eps (for eps >= 0), the first
path found will be at most eps from optimal.
If h(n) <= cost(n,g)×gamma (for gamma >= 1), the first
path found will be at most gamma times optimal.
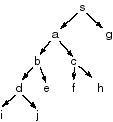
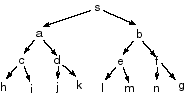
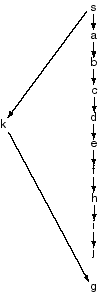
For each of the following, give a graph that is a tree (there is at
most one arc into any node), contains at most 15
nodes, and has at most two arcs out of any node.
- Give a graph where depth-first search is much more efficient (expands fewer nodes)
than breadth-first search.
- Give a graph where breadth-first search is much better than
depth-first search.
- Give a graph where A* search is more efficient than either
depth-first search or breadth-first search.
- Give a graph where depth-first search and breadth-first search
are both more efficient than A* search.
You must draw the graph and show the order of the neighbors (this is
needed for the depth-first search). Either give the arc costs and
heuristic function or state explicitly that you are drawing the graph
to scale and are using Euclidean distance for the arc costs and the
heuristic function.
In all of these graphs, we assume that we are on a plane, with
Euclidean distance (straight-line distance) as the arc cost and as the
heuristic function. We also assume that the neighbors are ordered
from left to right. The start node is s and the goal node is g.
- Give a graph where depth-first search is much more efficient (expands fewer nodes)
than breadth-first search.
Here depth-first search expands every node, whereas breadth-first
search expands three nodes:
- Give a graph where breadth-first search is much better than
depth-first search.
Here depth-first search expands every node, whereas breadth-first
search expands three nodes:
- Give a graph where A* search is more efficient than either
depth-first search or breadth-first search.
Here depth-first search and breadth-first
search expand every node, whereas A* search expands 4 nodes.
- Give a graph where depth-first search and breadth-first search
are both more efficient than A* search.
Here depth-first search expands three nodes, breadth-first search
expands 4, yet A* search expands every nodes.