CS422 Spring 2005
Assignment 5
Due: 2:00pm, Thursday 7 April 2005.
The aim of this assignment is to learn more about representing
knowledge and about inference in decision networks.
Please read and post to the bulletin in the course WebCT site for
hints and questions. Note that this assignment is designed to get you
to think and learn, not to test your pre-existing knowledge (or that
you have absorbed what has been covered in class). You will only learn
this stuff by trying it out. Please make sure you start this
assignment early!
Students have to make decisions about hum much to study for each
course. The aim of this question is to investigate using decision
networks to help them make such decisions for for a course.
Suppose students first have to decide to study for the midterm. They
can study a lot, study a little, or not study at all. Whether they
pass the midterm depends on how much they study and how difficult the
course is. As a first order approximation, they pass if they study
hard or if the course is easy and they study a bit. After receiving
their midterm grade, they have to decide how much to study for the
final exam. Again the final exam result depends on how much they
study and how difficult the course is. Their final grade depends on
which exams they pass; generally they get an A if they pass both
exams, a B if they only pass the final, a C if they only pass the
midterm and an F if they fail both. Of course there is lots of noise
in these general estimates.
Suppose that their final utility depends on their total effort and
their final grade. Suppose the total effort is obtained by adding the
effort in studying for the midterm and the final.
- Draw a decision network for a student decision based on the
above story.
- What is the domain of each variable?
- Give appropriate conditional probability tables.
- What is the best outcome (give this a utility of 100) and what
is the worst outcome (give this a utility of 0)?
- Give an appropriate utility function for a student who just wants to
pass. What is the optimal policy for this student?
- Give an appropriate utility function for a student who want to
do really well. What is the optimal policy for this student?
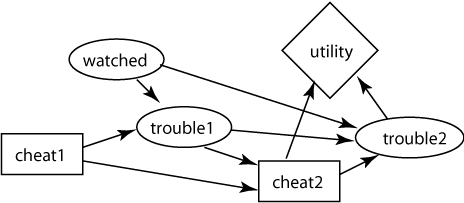
Consider the belief network:
The probabilities are available from the cs422
web site. This is supposed to model a decision about whether to cheat
at two different time instances.
- What is the optimal decision function for the variable cheat2? Show
what factors are created. Please try to do it
by hand, then check it with the CIspace applet.
- What is the optimal policy?
- What happens to the optimal policy if the probability of being watched goes up? What
happens to the optimal policy when the rewards for cheating are
reduced? What happens to the optimal policy when the instructor is
less forgiving (or forgetful) of previous cheating?
- How long did you spend on each question? Was it reasonable?
- What did you learn?
David Poole