CS422 Spring 2005
Assignment 4

Due: 2:00pm, Tuesday 15 March 2005.

The aim of this assignment is to learn more about representing knowledge and about inference in belief networks.

Please read and post to the bulletin in the course WebCT site for hints and questions. Note that this assignment is designed to get you to think and learn, not to test your pre-existing knowledge (or that you have absorbed what has been covered in class). You will only learn this stuff by trying it out. Please make sure you start this assignment early!

Question 1

Suppose we want to diagnose school student's addition of multi-digit binary numbers. Suppose we are only considering adding two two-digit numbers to form a three digit number.

That is, problems of the form:

A1 A0
+ B1 B0
C2 C1 C0
Here Ai, Bi and Ci are all binary digits.
  1. Suppose we want to model whether the student knows binary addition and whether they know how to carry. If they know how, they usually get the right answer, but sometimes make mistakes. If they don't know how to do either task, they just guess.

    What variables are needed to model binary addition and the errors students could make? You need to specify, in words, what each of the variables represents. Give a DAG that specifies the dependence of these variables.

  2. What are reasonable conditional probabilities for this domain?
  3. Implement this, for example using the belief network tool at:
    http://www.cs.ubc.ca/labs/lci/CIspace/.
    Test the implementation (don't forget to save your graph).

You need to give the graph, explain what each variable means, give the probability tables, and show how it works on a number of examples.

Question 2

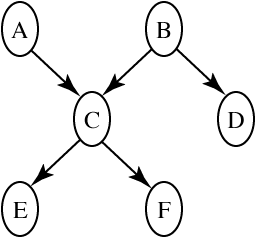
Consider the belief network:

Belief network

with Boolean variables (we will write A=true as a and A=false as ¬a) and the following conditional probabilities:
P(a) = 0.9
P(b) = 0.2
P(c|a,b) = 0.1
P(c|a,¬b) = 0.8
P(c|¬a,b) = 0.7
P(c|¬a,¬b) = 0.4
P(d| b) = 0.1
P(d|¬b) = 0.8
P(e|c) = 0.7
P(e|¬c) = 0.2
P(f|c) = 0.2
P(f|¬c) = 0.9
  1. Compute P(e) using variable elimination. Show the factors that are created for a given elimination ordering. Please try to do it by hand, then check it with the CIspace applet.
  2. Compute P(e|¬f) using variable elimination. How much of the previous computation can be reused? (You only need to show the factors that are different from those in part (a).

Question 3

Please attach this page to your assignment. This will be used to improve the course and the course materials (including the applet).
  1. Did you use the CIspace applet in this assignment?
  2. Did you use any other tools? (If so, what?)
  3. How did you learn to use the applet? (check all that apply)
    1. By watching the demonstrations in class.
    2. By looking through the CIspace help pages.
    3. By watching the video tutorials online.
    4. By asking others.
    5. By exploring the applet on your own.
    6. Other (please specify)
  4. How do you typically like to learn or feel you learn best (select all that apply):
    1. By reading textbooks or other text-based materials
    2. By studying visual or graphical material
    3. By studying worked out sample problems
    4. By watching problems being worked out/demonstrated in class
    5. By solving problems on your own
  5. Did the applet help make the concepts covered in class more clear?
  6. On a scale of 1 to 5, how easy was the applet to use? (1=very difficult, 5=very easy):
  7. On a scale of 1 to 5, how useful was the applet? (1=not at all useful, 5=very useful):
  8. On a scale of 1 to 5, how enjoyable was the applet? (1=not at all enjoyable, 5=very enjoyable):
  9. For each question in this assignment, say how long you spent on it. Was this reasonable?
    1. Question 1:
    2. Question 2:
    3. Question 3:
  10. Do you have any other comments about the assignment?
  11. What would you most like to see improved in the applet?
David Poole