Solution

1. Show how backtracking can be used to solve this problem, using the variable ordering A,B,C,D,E. To do this you should draw the search tree generated to find all answers. Indicate clearly the satisfying assignments. How many leaves are in the search tree generated?

   There are 232 leaves. The tree can be generated by the following Prolog program.

2. Is there a different variable ordering that results in a smaller tree? Give a variable ordering that results in the smallest tree. How many leaves are on this tree? Explain why you think this is the optimal ordering. (A good explanation is more important than actually finding the optimal ordering).

   Look at the variables. A reasonable strategy is a greedy (hillclimbing) strategy to select the variable that cuts the space most at any stage (I.e., you want to fail as quickly as possible). For example, a good ordering is A, D, C, E, B, which results in 56 leaves (see the tree).

3. Show how arc consistency can be used to solve this problem. To do this you need to:
   1. draw the constraint graph.

      

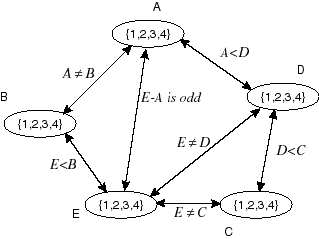
      Constraint Graph 
   2. show which elements of a domain are deleted at each step, and which arc is responsible for removing the element,

      Element Removed	Arc
      E=1	<E,B >
      B=4	<B,E >
      D=4	<D,C >
      C=1	<C,D >
      A=3,A=4	<A,D >
      D=1	<D,A >
      C=2	<C,D >

   3. show explicitly the constraint graph after arc consistency has stopped.

      

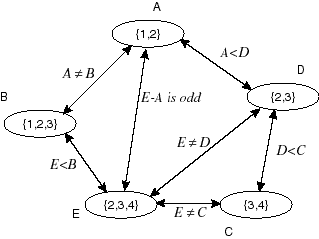
      Arc Consistent Constraint Net 
   4. show how splitting domains can be used to solve this problem. Assume we split the alphabetically first variable that has more than one element in its domain for any arc-consistent network. Include all arc consistency steps.

      Here is the results without the arc consisteny steps:

      A=1  B=2 solution (A=1, B=2, C=3, D=2, E=4}
           B=3 solution (A=1, B=3, C=3, D=2, E=4}
      A=2 failure