CS322 Fall 1997
Assignment 6 (fun and games)

Due: 1:30pm, Friday 17 October 1997.

Question 1

Consider the crossword puzzle:
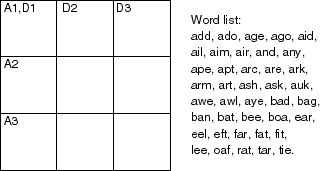
Place a letter in each square. You must find six three-letter words: three words read across (A1, A2, and A3) and three words read down (D1, D2, and D3). Each word must be chosen from the list of 40 possible words shown. You can solve it however you like, but please explain how you solved it. (This makes a good parlour game for the holiday Monday).

Please, please, please, don't tell anyone else the solution.

Solution: There are many ways to solve it.

Note that there are two solutions, and one is a mirror image of the other.

Question 2

Tic-tac-toe is a game played on a 3×3 grid. Two players, X and O, alternately place their mark in an unoccupied position. X wins if, at its turn, it can place an X in an unoccupied position to make three X's in a row. For example, from the state of the game
X O O
X
X O
X can win by moving into the left middle position.

Fred, Jane, Harold, and Jennifer have all written programs to determine if, given a state of the game, X can win in the next move. Each of them has decided on different representation of the state of the game. The aim of this question is to compare their representations.

Fred decided to represent a state of the game as a list of three rows, where each row was a list containing three elements, either x, o, or b (for blank). Fred represents the above state as the list

[[x,o,o],[b,c,b],[x,b,o]].

Jane decided that each position on the square could be described by two numbers, the position across and the position up. The top left X is in position pos(1,3), the bottom left X is in position pos(1,1), and so forth. She then decided to represent the state of the game as a pair ttt(XPs,OPs) where XPs is the list of X's positions and OPs is the list of O's positions. Thus Jane represented the above state as

ttt([pos(1,3), pos(2,2), pos(1,1)], [pos(2,3), pos(3,3), pos(3,1)]).

Harold and Jennifer both realized that the positions on the tic-tac-toe board could be represented in terms of a so-called magic square:

6 7 2
1 5 9
8 3 4
Based on this representation, the game is transformed into one where the two players alternately select a digit. No digit can be selected twice, and the player who first selects three digits summing to 15 wins.

Harold decides to represent a state of game as a list of nine elements, each of which is x, o, or b, depending on whether the corresponding position in the magic square is controlled by X, controlled by O, or is blank. Thus Harold represents the game state above as the list:

[b, o, b, o, x, x, o, x, b].

Jennifer decides to represent the game as a pair consisting of the list of digits selected by X and the list of digits selected by O. She represented the state of the game above as

magic([6, 5, 8], [7,2, 4]).
  1. For each of the four representations, write the relation such as x_won_fred(State), with the intended interpretation that X has won the game in state State based on Fred's representation (and similarly for the other three representations).

    You can use the relations "V is E" which is true if arithmetic expressions E has value V, "X != Y" which is true if ground terms X and Y are not identical, member(E,L) which is true of E is a member of list L, and any other predicates you want to define.

  2. Which do you think is the best representation? Explain why. Can you suggest a better representation?

Solution Code.

Question 3

For each question in this assignment, say how long you spent on it. (You can get a bonus mark if you answer this completely).