3 Comparting Different Search Strategies

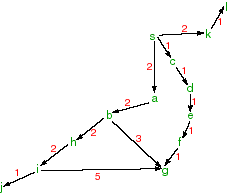
Suppose the neighbours are given by the following relations:

neighbours(s,[a,c,k]).
neighbours(a,[b]).
neighbours(b,[h,g]).
neighbours(c,[d]).
neighbours(d,[e]).
neighbours(e,[f]).
neighbours(f,[g]).
neighbours(g,[]).
neighbours(h,[i]).
neighbours(i,[j]).
neighbours(j,[]).
neighbours(k,[l]).
neighbours(l,[]).

h(a,2).     h(b,3).
h(c,4).     h(d,3).
h(e,2).     h(f,1).     
h(g,0).     h(h,4).     
h(i,5).     h(j,6).     
h(k,5).     h(l,6).     
h(s,4).     

1. Depth-first search
2. Breadth-first search
3. Least-cost first search
4. Best-first search
5. A^* search

1. What is the final path found?
2. How many nodes were expanded?
3. Explain why it selected nodes during the search that were not on the shortest path from s to g.
4. Explain why it may have been led astray in the final solution. (Either state that it found the shortest part, or explain why the shortest path was not found).