Go up to Top
Go forward to 2 Searching on a simple graph

1 Finding Paths in a Grid

Consider the problem of finding a path in the grid shown below from the position s to the position g. The robot can move on the grid horizontally and vertically, one square at a time (each step has a cost of one). No step may be made into a forbidden shaded area.

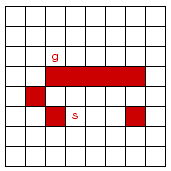
On the grid, number the nodes in the order in which they are removed from the frontier in a depth-first search from s to g, given that the order of the operators you will test is: up, left, right, then down. Assume there is a cycle check.
Number the nodes in order in which they are taken off the frontier for an A^* search for the same graph. Manhattan distance should be used as the heuristic function. That is, h(n) for any node n is the Manhattan distance from n to g. The Manhattan distance between two points is the distance in the x-direction plus the distance in the y-direction. It corresponds to the distance traveled along city streets arranged in a grid. For example, the Manhattan distance between g and s is 4. What is the path that is found by the A^* search?
Assume that you were to solve the same problem using dynamic programming. Give the dist value for each node, and show which path is found.
Based on this experience, discuss which algorithms are best suited for this problem.
Suppose that the graph extended infinitely in all directions. That is, there is no boundary, but s, g, and the forbidden area are in the same relative positions to each other. Which methods would no longer find a path? Which would be the best method, and why?