Computational Intelligence

Online Slides

October 29, 2002

These are slides from Computational Intelligence, A Logical Approach, Oxford University Press, 1998. Copyright ©David Poole, Alan Mackworth, Randy Goebel and Oxford University Press, 1999-2002. You may prefer the pdf interface for which these slides were designed (you can read pdf files using the free acrobat reader).

Chapter 7, Lecture 1

Equality

Sometimes two terms denote the same individual.
Example: Clark Kent & superman. 4×4 & 11+5.
The projector we used last Friday & this projector.
Ground term t₁ equals ground term t₂, written t₁=t₂, is true in interpretation I if t₁ and t₂ denote the same individual in interpretation I.

Equality doesn't mean similarity

chair1 != chair2
chair_on_right = chair2
chair_on_right is not similar to chair2, it is chair2.

Why is equality important?

In a doctor's office, the doctor wants to know if a patient is the same patient that she saw last week (or is his twin sister).
In a criminal investigation, the police want to determine if someone is the same person as the person who committed some crime.
When buying a replacement switch, an electrician may want to know if it was built in the same factory as the switches that were unreliable. (And if it is a different switch to the one that was replaced the previous time).

Allowing Equality Assertions

Without equality assertions, the only thing that is equal to a ground term is itself.
This can be captured as though you had the assertion X=X. Explicit equality never needs to be used.
If you allow equality assertions, you need to derive what follows from them. Either:
- axiomatize equality like any other predicate
- build special-purpose inference machinery for equality

Axiomatizing Equality

X=X.
X=Y <- Y=X.
X=Z <- X=Y & Y=Z.

For each n-ary function symbol f there is a rule of the form

f(X_1,...,X_n)=f(Y_1,..., Y_n) <-
X_1=Y_1 & ··· & X_n=Y_n.

For each n-ary predicate symbol p, there is a rule of the form

p(X_1,...,X_n) <-
p(Y_1,..., Y_n) & X_1=Y_1 & ··· & X_n=Y_n.

Special-Purpose Equality Reasoning

paramodulation: if you have t₁=t₂, then you can replace any occurrence of t₁ by t₂.

Treat equality as a rewrite rule, substituting equals for equals.

You select a canonical representation for each individual and rewrite all other representations into that representation.

Example: treat the sequence of digits as the canonical representation of the number.

Example: use the student number as the canonical representation for students.

Unique Names Assumption

The convention that different ground terms denote different individuals is the unique names assumption.

For every pair of distinct ground terms t₁ and t₂, assume t₁ != t₂, where " != " means "not equal to."

Example: For each pair of courses, you don't want to have to state, math302 != psyc303, ...

Example: Sometimes the unique names assumption is inappropriate, for example 3+7 != 2×5 is wrong.

Axiomatizing Inequality for the UNA

c != c' for any distinct constants c and c'.
f(X₁,...,X_n) != g(Y₁,...,Y_m) for any distinct function symbols f and g.
f(X₁,...,X_n) != f(Y₁,...,Y_n) <- X_i != Y_i, for any function symbol f. There are n instances of this schema for every n-ary function symbol f (one for each i such that 1 <= i <= n).
f(X₁,...,X_n) != c for any function symbol f and constant c.
t != X for any term t in which X appears (where t is not the term X).

Top-down procedure and the UNA

Inequality isn't just another predicate. There are infinitely many answers to X != f(Y).
If you have a subgoal t₁ != t₂, for terms t₁ and t₂ there are three cases:
- t₁ and t₂ don't unify. In this case, t₁ != t₂ succeeds.
- t₁ and t₂ are identical including having the same variables in the same positions. Here t₁ != t₂ fails.
- Otherwise, there are instances of t₁ != t₂ that succeed and instances of t₁ != t₂ that fail.

Implementing the UNA

Recall: in SLD resolution you can select any subgoal in the body of an answer clause to solve next.
Idea: only select inequality when it will either succeed or fail, otherwise select another subgoal. Thus you are delaying inequality goals.
If only inequality subgoals remain, and none fail, the query succeeds.

Inequality Example

notin(X,[]).
notin(X,[H|T]) <- X != H & notin(X,T).
good_course(C) <- course(C) & passes_analysis(C).
course(cs312).
course(cs444).
course(cs322).
passes_analysis(C) <- something_complicated(C).
? notin(C,[cs312,cs322,cs422,cs310,cs402])
& good_course(C).

Chapter 7, Lecture 2

Complete Knowledge Assumption (CKA)

Sometimes you want to assume that a database of facts is complete. Any fact not listed is false.
Example: Assuming a database of enrolled(S,C) relations is complete, you can define empty_course(C).
The definite clause RRS is monotonic: adding clauses doesn't invalidate a previous conclusion.
With the complete knowledge assumption, the system is nonmonotonic: a conclusion can be invalidated by adding more clauses.

CKA: propositional case

Suppose the rules for atom a are
a <- b₁.

...

a <- b_n.

or equivalently: a <- b₁ or ... or b_n
Under the CKA, if a is true, one of the b_i must be true:
a -> b_1 or ... or b_n.
Under the CKA, the clauses for a mean Clark's completion:
a <-> b_1 or ... or b_n

CKA: Ground Database

Example: Consider the relation defined by:

student(mary).
student(john).
student(ying).

The CKA specifies these three are the only students:

student(X) <-> X=mary or X=john or X=ying.

To conclude ¬student(alan), you have to be able to prove

alan != mary & alan != john & alan != ying

This needs the unique names assumption.

Clark Normal Form

The Clark normal form of the clause:

p(t_1,...,t_k) <- B

is the clause

p(V_1,...,V_k) <-
exist W_1...exist W_m V_1=t_1 & ... & V_k =t_k & B,

where V₁,...,V_k are k different variables that did not appear in the original clause.

W₁,...,W_m are the original variables in the clause.

Clark normal form: example

The Clark normal form of:
room(C,room208) <-
cs_course(C) & enrollment(C,E) & E<120.
is
room(X,Y) <- exist C exist E X=C & Y=room208 &
cs_course(C) & enrollment(C,E) & E<120.

Clark's Completion of a Predicate

Put all of the clauses for p into Clark normal form, with the same set of introduced variables:

p(V_1,...,V_k) <- B_1
...
p(V_1,...,V_k) <- B_n

This is the same as: ~~ p(V₁,...,V_k) <- B₁ or ... or B_n.

Clark's completion of p is the equivalence

p(V_1,...,V_k) <-> B_1 or ... or B_n,

That is, p(V₁,...,V_k) is true if and only if one B_i is true.

Clark's Completion Example

Given the mem function:

mem(X,[X|T]).
mem(X,[H|T]) <- mem(X,T).

the completion is

mem(X,Y) <-> (exist T Y=[X|T]) or
(exist H exist T Y=[H|T] & mem(X,T))

Clark's Completion of a KB

Clark's completion of a knowledge base consists of the completion of every predicate symbol, along with the axioms for equality and inequality.
If you have a predicate p defined by no clauses in the knowledge base, the completion is p <-> false. That is, ¬p.
You can interpret negations in the bodies of clauses. ~ p means that p is false under the Complete Knowledge Assumption. This is called negation as failure.

Using negation as failure

Previously we couldn't define empty_course(C) from a database of enrolled(S,C).

This can be defined using negation as failure:

empty_course(C) <-
      course(C) &
      ~ has_Enrollment(C).
has_Enrollment(C) <-
     enrolled(S,C).

Bottom-up NAF proof procedure

C:={};

repeat

either select "h <- b₁ & ... & b_m" in KB such that

b_i in C for all i, and h not in C;

C:=C union {h}

or select h such that

for every rule "h <- b₁ & ... & b_m" in KB

either for some b_i, ~ b_i in C

or some b_i= ~ g and g in C

C:=C union { ~ h}

until no more selections are possible

Negation as failure example

p <- q & ~ r.
p <- s.
q <- ~ s.
r <- ~ t.
t.
s <- w.

Top-Down NAF Procedure

If the proof for a fails, you can conclude ~ a.
Failure and success can be defined recursively:
- Suppose you have rules for atom a:
  a <- b₁
  
  ...
  
  a <- b_n
  
  If each body b_i fails, a fails.
  If one body, b_i succeeds, a succeeds.
- A body fails if one of the conjuncts in the body fails.
  A body succeeds if all of the conjuncts succeed.
- If a fails, ~ a succeeds. If a succeeds ~ a fails.

Free Variables in Negation as Failure

Example:

p(X) <- ~ q(X) & r(X).
q(a).
q(b).
r(a).
r(c).

There is only one answer to the query ?p(X), namely X=c.

For calls to negation as failure with free variables, you need to delay negation as failure goals that contain free variables until the variables become bound.

Floundering Goals

If the variables never become bound, a negated goal flounders.

In this case you can't conclude anything about the goal.

Example: Consider the clauses:

p(X) <- ~ q(X)
q(X) <- ~ r(X)
r(a)

and the query

?p(X).

Chapter 7, Lecture 3

Integrity Constraints

In the electrical domain, what if we predict that a light should be on, but observe that it isn't?
What can we conclude?
We will expand the definite clause language to include integrity constraints which are rules that imply false, where false is an atom that is false in all interpretations.
This will allow us to make conclusions from a contradiction.
A definite clause knowledge base is always consistent. This won't be true with the rules that imply false.

Horn clauses

An integrity constraint is a clause of the form
false <- a_1 & ... & a_k
where the a_i are atoms and false is a special atom that is false in all interpretations.
A Horn clause is either a definite clause or an integrity constraint.

Negative Conclusions

Negations can follow from a Horn clause KB.
The negation of alpha, written ¬alpha is a formula that
- is true in interpretation I if alpha is false in I, and
- is false in interpretation I if alpha is true in I.
Example:
KB={
false <- a & b.

a <- c.

b <- c.
} KB ¬c.

Disjunctive Conclusions

Disjunctions can follow from a Horn clause KB.
The disjunction of alpha and beta, written alpha or beta, is
- true in interpretation I if alpha is true in I or beta is true in I (or both are true in I).
- false in interpretation I if alpha and beta are both false in I.
Example:
KB={
false <- a & b.

a <- c.

b <- d.
} KB ¬c or ¬d.

Questions and Answers in Horn KBs

An assumable is an atom whose negation you are prepared to accept as part of a (disjunctive) answer.
A conflict of KB is a set of assumables that, given KB imply false.
A minimal conflict is a conflict such that no strict subset is also a conflict.

Conflict Example

Example: If {c,d,e,f,g,h} are the assumables

KB={
false <- a & b.

a <- c.

b <- d.

b <- e.
}

{c,d} is a conflict
{c,e} is a conflict
{c,d,e,h} is a conflict

Using Conflicts for Diagnosis

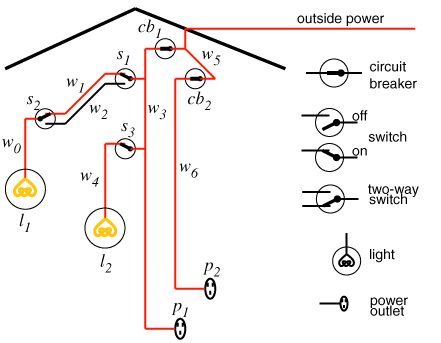
Assume that the user is able to observe whether a light is lit or dark and whether a power outlet is dead or live.
A light can't be both lit and dark. An outlet can't be both live and dead:
false <=dark(L) &lit(L).
false <=dead(L) &live(L).
Make ok assumable: assumable(ok(X)).
Suppose switches s₁, s₂, and s₃ are all up:
up(s₁). up(s₂). up(s₃).

Electrical Environment

lit(L) <=light(L)&ok(L)&live(L).
live(W) <=connected_to(W,W_1)&live(W_1).
live(outside)<=true.
light(l_1)<=true.
light(l_2)<=true.
connected_to(l_1,w_0)<=true.
connected_to(w_0,w_1) <=up(s_2)&ok(s_2).
connected_to(w_1,w_3) <=up(s_1)&ok(s_1).
connected_to(w_3,w_5) <=ok(cb_1).
connected_to(w_5,outside)<=true.

If the user has observed l₁ and l₂ are both dark:
dark(l₁).~dark(l₂).
There are two minimal conflicts:
{ok(cb_1),ok(s_1),ok(s_2),ok(l_1)} and
{ok(cb_1),ok(s_3),ok(l_2)}.
You can derive:
¬ok(cb_1) or ¬ok(s_1) or ¬ok(s_2) or ¬ok(l_1)
¬ok(cb_1) or ¬ok(s_3) or ¬ok(l_2).
Either cb₁ is broken or there is one of six double faults.

Diagnoses

A consistency-based diagnosis is a set of assumables that has at least one element in each conflict.
A minimal diagnosis is a diagnosis such that no subset is also a diagnosis.
Intuitively, one of the minimal diagnoses must hold. A diagnosis holds if all of its elements are false.
Example: For the proceeding example there are seven minimal diagnoses: {ok(cb₁)}, {ok(s₁),ok(s₃)}, {ok(s₁),ok(l₂)}, {ok(s₂),ok(s₃)},...

Conclusions are pairs <a,A>, where a is an atom and A is a set of assumables that imply a.
Initially, conclusion set C={<a,{a}>:a is assumable}.
If there is a rule h <- b₁ & ... & b_m such that
for each b_i there is some A_i such that <b_i,A_i> in C, then <h,A₁ union ... union A_m> can be added to C.
If <a,A₁> and <a,A₂> are in C, where A₁ strict subset A₂, then <a,A₂> can be removed from C.
If <false,A₁> and <a,A₂> are in C, where A₁ subset A₂, then <a,A₂> can be removed from C.

Bottom-up Conflict Finding Code

C:={<a,{a}>:a is assumable };

repeat

select clause "h <- b₁ & ... & b_m" in T such that

<b_i,A_i> in C for all i and

there is no <h,A'> in C or <false,A'> in C

such that A' subset A where A=A₁ union ... union A_m;

C:=C union {<h,A>}

Remove any elements of C that can now be pruned;

until no more selections are possible

Integrity Constraints in Databases

Database designers can use integrity constraints to specify constraints that should never be violated.
Example: A student can't have two different grades for the same course.
false <-
      grade(St,Course,Gr_1) &
      grade(St,Course,Gr_2) &
      Gr_1 != Gr_2.
When false is derived, how can be used to debug the KB.