Section 2: Natural Recursion

Table of Contents > Chapter 2 > Section 2

We are now in a position to introduce the following data definition for a list:

# ListOfX is one of:
# - []
# - [X] + ListOfX
# interp. a list of values of type X

L1 = []
L2 = [4, 3, 6]

# def fn_for_lox(lox):
#    if lox == []:
#        return ...
#    else:
#        return ...lox[0]...fn_for_lox(lox[1:])

Note that this is a parameterized data type. X is a type parameter that represents the type of data that will be stored in the list. The above data definition is so commonly used that we assign it the special notation (listof X). So, for example, we could have a (listof str) or (listof int) or even (listof Account).

Let's examine this data definition a little more closely...

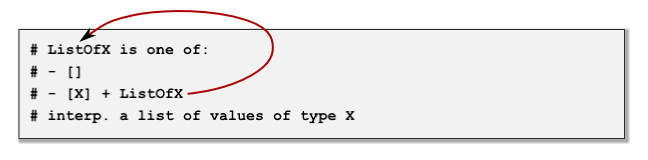
Notice that the types comment is self-referential. We define ListOfX in terms of itself, as indicated by the arrow above. Now notice that we have a corresponding natural recursion in the function template...

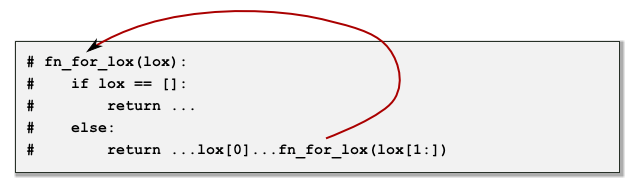
This is an example of how the shape of the data governs the shape of the corresponding program. There is another sense in which this is true for this data definition. Notice that the data definition has two clauses and that the corresponding function template has two corresponding clauses that are expressed with an if-else statement.

Now let's suppose that we wish to design a function that computes the sum of a list of integers. By applying the HtDF design recipe, we arrive at the code found in .

Now let's use our function to compute the sum of some lists of integers. Note that we use the built-in Python functions list and range to quickly generate some sample lists. In general, list(range(n)) produces the list

[0, 1, 2,
        ..., n - 1]

.

>>> sum_loi((list(range(10)))
45
>>> sum_loi(list(range(100)))
4950
>>> sum_loi(list(range(1000)))
...
RuntimeError: maximum recursion depth exceeded

The final call results in a runtime error due to the fact that the computation exceeds the maximum recursion depth allowed by the Python interpreter. Note that each time we make a recursive call to the sum_loi function, the interpreter has to accumulate another piece of the sum. So, if we pass the list [4, 2, 6, 5, 1] as an argument to the sum_loi function, the following computation is ultimately accumulated in memory:

(4 + (2 + (6 + (5 + 1))))
The brackets are included to illustrate the order in which the computation is performed. This accumulation consumes memory and memory is a finite resource. Python therefore imposes a limit on the depth of the recursive calls that can be made. This does not mean that recursion is not useful. Recursion represents a natural design for functions that consume data that is self-referential. However, if the size of that data is large, we may find that we exceed the depth of recursive calls that is allowed in Python. In the next section, we consider the use of tail-recursion to determine if it can be used as a work-around for the limited depth of recursive calls. (It won't, but it will get us one step closer to a solution to the problem!)