Section 2: Numeric Data

Table of Contents > Chapter 1 > Section 2

Representing numeric information in Python

The Python programming language provides many built-in data types. Our purpose is not to consider all of them but to provide an introduction to a commonly used subset.

In CPSC 110 the languages that you learned are such that mathematical computations are exact whenever possible. This is one of the features of the programming languages used in CPSC 110 that allowed you to focus on design principles. Unfortunately, mathematical computations in many other programming languages are not exact, in general. The Python programming language has two commonly used data types that can represent real numbers in the world: int and float. The int data type is used to represent integer values while the float data type can be used to represent integer and non-integer values.

One important difference between the two is that computations on data of type int are always exact, whereas those on data of type float are, in general, only an approximation to the exact value.

We have stated that the float data type can represent integer and non-integer values. This raises a question. How do we distinguish between an integer value represented by an int versus one that is represented by a float? The answer is to include a decimal point if and only if you want to represent the integer value as a float. Python’s built-in type function can be used to determine the type of a given value. Consider the following:

>>> type( 4 ) 
<type 'int'>

>>> type( 4.0 )
 <type 'float'>

>>> type( 4. ) 
<type 'float'>

Another important observation is that binary arithmetic operations on data of type int, produce a value of type int, except in the case of division, where a value of type float is produced. So, for example,

>>> 15 / 5 
3.0 # NOT 3

>>> 15 / 4 
3.75

There may be situations where you want to produce an integer result when dividing one integer by another. To do this in Python, use the floor division // operator. This operator divides one integer by another and rounds down to the nearest integer, as illustrated in the following examples:

>>> 6 // 3
 2              # NOT 2.0

>>> 15 // 4 
3            # 3.75 rounded down to 3

>>> -15 // 4
-4             # -3.75 rounded down to -4

When working with numeric information, you must now think carefully about how to represent that information as data in your program. Data of type int should be used to represent integer values whenever possible, as computations on data of type int are always exact.

Designing functions that consume numeric data

Before we learn how to design functions from scratch, we'll take a look at a function that has already been designed for us. The simple function illustrated in Interactive 1.1 consumes a value of type int and produces the square of that value (another int). Explore this function by hovering your mouse over the different components.

This is the signature. It indicates the type of data consumed and the type of data produced. In this case, the function consumes an int and produces an int.

This is the purpose statement. It provides a concise description of what the function produces.

This is a test. It expresses the fact that when we call the function with the argument 0, we expect the function to produce the value 0.

This is a test. It expresses the fact that when we call the function with the argument 3, we expect the function to produce the value 9.

This is the body of the function. It contains the statements to be executed when the function is called.


              def sqr( num ):
                  """

                   
                  int -> int

                

                   
                  Produces the square of num 

                

                   
                  >>> sqr( 0 )

                      0 

                

                   
                  >>> sqr( 3 )

                      9

                    """

                 
                return num * num

Interactive 1.1

Although you may not yet be familiar with Python syntax, you can probably identify the following elements of the How to Design Functions (HtDF) recipe: signature, purpose statement, tests and body. Investigate the interactive image to ensure that you can identify these elements.

Note that we use the def keyword to define a function. The return keyword is used to specify the value that is ultimately produced when the function is called with the given argument(s). Note that in addition to specifying the value produced by the function, a return statement terminates the call to the function.

Finally note that we have a multi-line comment statement that starts with """ and ends with """. This multi-line comment statement includes documentation such as the signature, purpose and tests. Given that the tests are designed as part of the function's documentation, they are known as doctests or document tests.

Designing doctests

Each doctest starts with >>> and is followed by a call to the function. Note that the space after the three angle brackets is required. On the next line we specify the value that we expect to see, if the call were made from a Python shell. This is typically the value produced by the function. We can include as many doctests as are needed.

There are some pitfalls when using doctests. Note that we must specify the expected value as a literal value. We cannot use expressions to compute the value. So, in the second doctest provided in Interactive 1.1, you cannot write the following:

>>> sqr( 3 )
 3 * 3 # this won't work

You must also be careful not to include any trailing spaces after the expected value, as everything you enter on the second line of the test must be produced by the function if the test is to pass!

Function Templates

Recall that the design of a function template is based on the type of data that the function consumes. Data of type int and float are examples of built-in, atomic data. The template for a function operating on atomic data is:

def fn_for_atmc( a ): 
return ...a

Recall that ... stands for do something with. So this template conveys the fact that to determine the value produced by the function we must do something with the value it consumes. If the function consumes more than one atomic data, we extend the function template in the natural way:

def fn_for_atmc( a, b, c ): 
return ...a ...b ...c

How to Design Functions (HtDF) Recipe

The recipe for how to design functions is very similar to the one you encountered in CPSC 110 but the syntax is somewhat different. As you read through this section, focus on the fact that conceptually you are learning nothing new. Try to map everything you see here onto the design recipe that you saw in CPSC 110.

Use the def keyword to define the function header. This includes the function's name and parameter list.
Write the function's documentation including:

signature
purpose statement

Write a stub that produces a default value whose type matches the type of data that the function produces, as specified in the function signature.
Design tests and add them to the function's documentation in the form of doctests.
Run your program and remove any syntax errors. Note that at least one test is expected to fail, in general, as we have only a stub in place at this point.
Replace the stub with the template for a function that consumes data of the type specified by the function signature.
Complete the template.
Run the tests and debug your program until all tests pass.

Now that we have established the recipe for designing functions in Python, let's design one from scratch. Suppose we want to design a function that determines the area of a rectangle given the rectangle's width and height. We assume that the rectangle is to be drawn on the screen and has dimensions that are integer values. The width and height provide us with information about the world. We must decide how that information is to be represented as data in our program. Given that the dimensions of the rectangle are integer values, it is natural to represent the width and height as data of type int in our program. Our program will produce data of type int that represents the corresponding area of the rectangle. The following diagram illustrates how information in the world is represented as data in our program and how data in our program is interpreted as information in the world for the particular case where we wish to compute the area of a rectangle of width 20cm and height 10cm.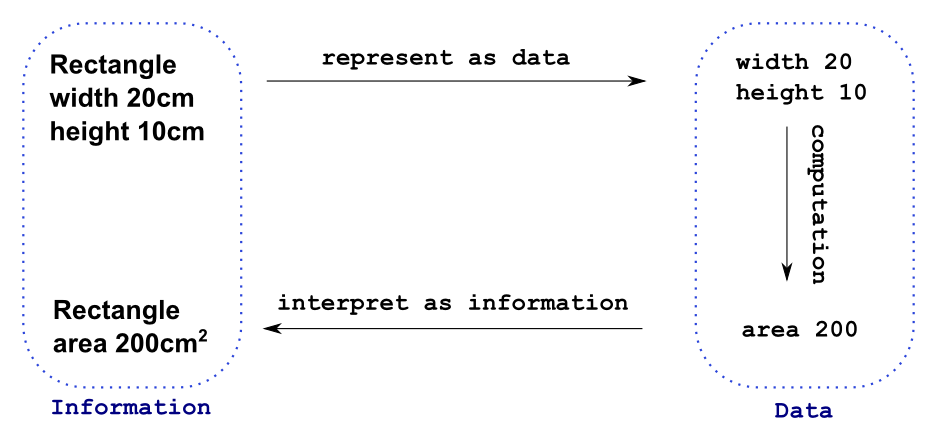

Information vs. Data

Now we can focus on the design of the function. This function performs a computation that takes us from the two integer values that represent the width and height of the rectangle to another integer value that we will interpret as the area of the rectangle.

Here's the final product:

def rect_area( width, height ):
    """
    int, int -> int

    Produces the area of a rectangle of
    the given width and height

    >>> rect_area( 0, 0 )
    0

    >>> rect_area( 10, 20 )
    200
    """
    return width * height

Take some time to study the design of the function above. It's a fairly straightforward example but it's important that you familiarize yourself with Python's syntax.

Now let's modify the problem specification and make the reasonable supposition that the width and height of the rectangle are not necessarily integer values. In this case, we choose to represent the width and height using data of type float. The function will then produce a float that we interpret as the area of the rectangle. This version of the function is presented below. Compare it with the earlier version and note that the body of the function is identical!

def rect_area( width, height ):
    """
    float, float -> float

    Produces the area of a rectangle of
     the given width and height

    >>> rect_area( 0.0, 0.0 )
    0.0

    >>> rect_area( 10.0, 20.0 )
    200.0
    """
    return width * height

Notice that we've been careful to use data of type float rather than data of type int for the values consumed and the values produced when designing our tests. It is important to realize that 0.0 is not the same as 0. If we specify that 0 is the expected value when the function actually produces 0.0, the test will fail.

We now have two versions of our rect_area function that are very similar. In fact, the only points of variation are the type of data that the function consumes and the type that it produces. We will now introduce the Real data type. It is a more abstract, numeric data type that encompasses the types int and float. By this we mean that values of type int and values of type float are both considered to be values of type Real. We will use the Real data type whenever we have values that could be of type int or of type float. The following function, that uses this more abstract data type, therefore takes the place of the two earlier versions:

def rect_area( width, height ):
    """
    Real, Real -> Real

    Produces the area of a rectangle of  
    the given width and height

    >>> rect_area( 0, 0 )
    0

    >>> rect_area( 10, 20 )
    200

    >>> rect_area( 10.5, 2.0 )
    21.0
    """
    return width * height

Given that the Real data type encompasses ints and floats, notice that we have at least one test that calls the function with arguments of type int and at least one other that employs arguments of type float.

Designing tests with values of type `float`

We have already commented on the fact that computations on data of type


        float

are not exact, in general. For this reason, we have to be careful when designing tests where the expected value is a float. In such cases we cannot expect the function to necessarily produce the exact value. In the tests that we designed for our rect_area function above, we got lucky - the function happened to produced the exact value when given the arguments 10.5 and 2.0. However, it's not hard to construct an example where the value produced by the function is not exact. For example, the following test will fail:

>>> rect_area( 0.1, 0.1 )
 0.01

The value produced by the function is actually 0.010000000000000002 - a very good approximation to 0.01, of course, but not the exact value.

When designing tests for functions that produce data of type float, we require the value produced to be only close enough to the expected value. So, in the example above, rather than stating that the expected value is 0.01, we have to design our test in such a way that the test will pass whenever the actual value produced is close enough to the expected value. We achieve this by requiring that the distance between the actual and expected values is small.

Our test therefore becomes:

>>> act = rect_area( 0.1, 0.1 )
 >>> exp = 0.01 
>>> abs( act - exp ) < abs( exp ) * EPS 
True

where EPS is a constant whose value is something small, like 1.0e-6. Note that the actual value produced is assigned to the variable act and the expected value is assigned to the variable exp. This test will pass only when the distance between the actual and expected values is within 1.0e-6 of the size of the expected value.

The set of values for which the test passes are represented by the blue shaded region in the following diagram:

Actual vs. Expected Value

The final version of our rect_area function is presented in