Sample problems for tutorial #8

1. It is possible to implement a queue using a pair of stacks as follows:

   • Enqueue(x) pushes x on stack #1.
   • Dequeue() first checks to see if stack #2 contains any elements. If so, it returns stack2.pop(). Otherwise, if first transfers every element from stack #1 onto stack #2 by calling stack2.push(stack1.pop()) as many times as necessary, and then it returns stack2.pop().

   Using amortized analysis, prove that the worst-case running time of any sequence of n enqueue and dequeue operations is in O(n).

2. In this problem, we consider a sequence of n successor operations on a binary search tree. Recall that the successor operation finds the node whose key would immediately follow the key stored in the current node if we listed the keys stored in the tree in order. For instance, in the following tree, the successor of the node with key 44 is the node with key 54, while the successor of the node with key 19 is the node with key 30.

   

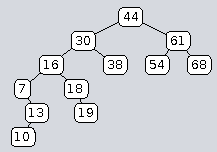
   The successor operation needs to handle two separate cases:

   • If the current node has a right child (for instance the node with key 44), then it goes right once, and then left as long as possible.
   • If the current node has no right child (for instance the node with key 19), then it goes up until it arrives at a node from its left child.

   Here is Java code for this operation:

   public BinaryTreeNode<ElementType> getSuccessor(BinaryTreeNode<ElementType> node)
   {
       if (node.getRightChild() != null)
       {
           return minimum(node.getRightChild());
       }
       while (node.getParent() != null && node == node.getParent().getRightChild())
       {
           node = node.getParent();
       }
       return node.getParent();
   }
   
   public BinaryTreeNode<ElementType> minimum(BinaryTreeNode<ElementType> node)
   {
       while (node.getLeftChild() != null)
       {
           node = node.getLeftChild();
       }
       return node;
   }
   

   Using the potential method, prove that a sequence of n successor operations on a binary search tree with n elements, starting from an unspecified element that is before the first element of the tree (you can think of adding a node "null" that has no left child, and the real root as its right child, and then starting at this "null" node) will run in O(n) time.

   Hint 1: use Φ(D_i) = r_i + (n - l_i) where r_i is the number of "right edges" (edges that go from a node to its right child) on the path from the root of the tree to the current node and l_i is the number of "left edges" on the same path.

   Hint 2: if Φ(D₀) ≠ 0 then the expression Φ(D₀) + Σ cost_am(op_i) is an upper bound on the sum of the real costs of the n operations.