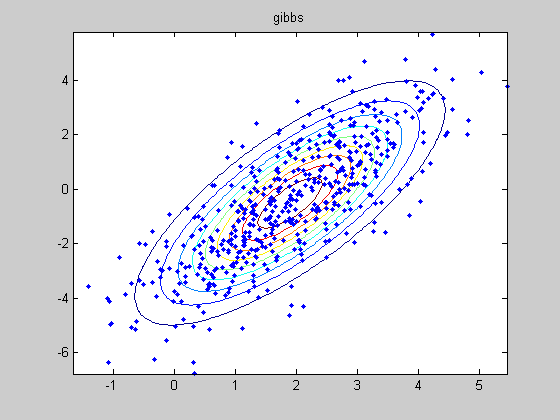
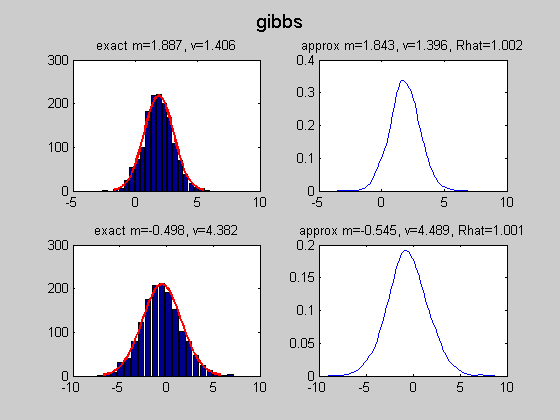
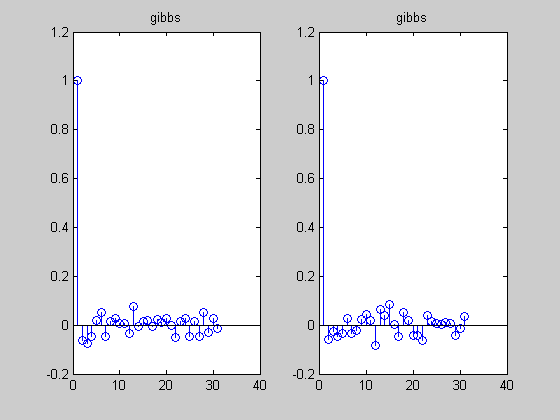
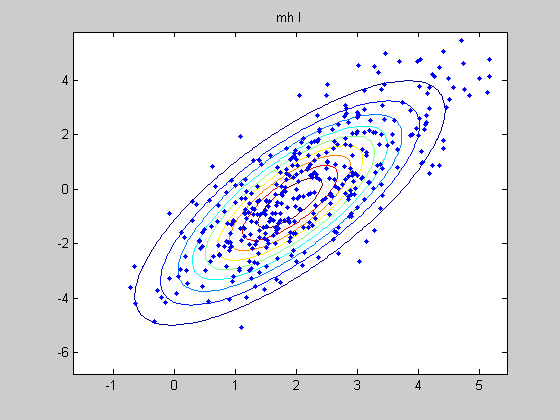
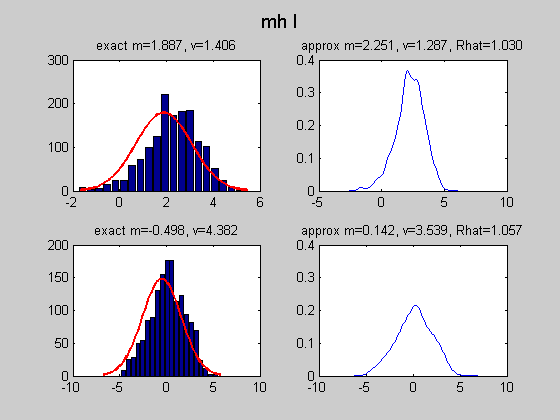
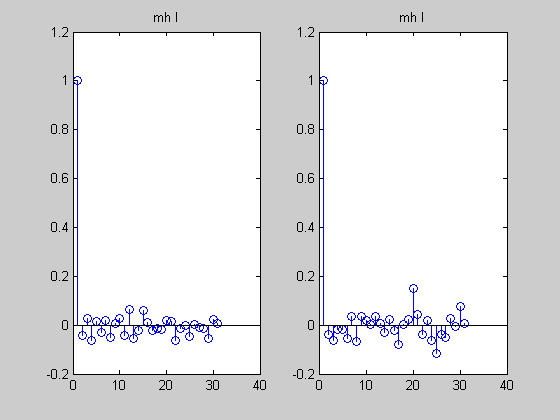
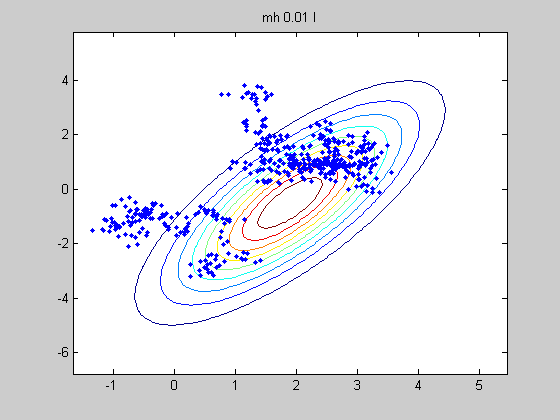
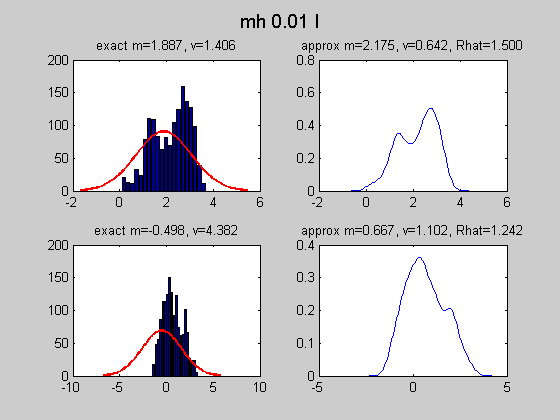
MCMC Sampling from a multivariate Gaussian conditioned on data

We use a N(0, sigma*eye(2)) proposal and see the effect of changing sigma We also compare to Gibbs sampling

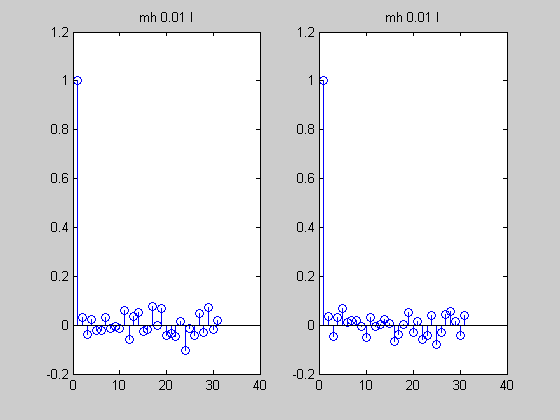
%#testPMTK

% Compared to mcmcMvn2d which calls the sampling routines
% directly, rather than using engines and calling the 'marginal' method

setSeed(0);
d = 5;
Sigma = randpd(d);
mu = randn(d,1);
mFull = MvnDist(mu, Sigma);
H = 1:2;
V = 3:d;
data = randn(1,length(V));
margExact = marginal(mFull, {1, 2, [1 2]}, V, data);% p(h|V=v) is a 2d Gaussian


N = 500;
mcmc{1} = MvnDist(mu, Sigma, 'infEng', GibbsInfEng('verbose', true, 'Nsamples', N));
h = length(H); % num hidden
mcmc{2} = MvnDist(mu, Sigma, 'infEng', ...
  MhInfEng('Nsamples', N, 'verbose', true, 'proposal', @(x) mvnrnd(x, 1*eye(h))));
mcmc{3} = MvnDist(mu, Sigma, 'infEng', ...
  MhInfEng('Nsamples', N, 'verbose', true, 'proposal', @(x) mvnrnd(x, 0.01*eye(h))));

%targetFn = @(x) logprob(MvnDist(mu,Sigma), x, false);
%initFn  = @()  mvnrnd(mu, Sigma);

names= {'gibbs', 'mh I', 'mh 0.01 I'};

for j=1:length(mcmc)
    ttl = names{j};
    figure;
    plot(margExact{3}, 'useContour', 'true');
    hold on
    S = sample(mcmc{j}, N, V, data);
    plot(S(:,1), S(:,2), '.');
    title(ttl)
    drawnow


    figure;
    [margApprox, junk, convDiag] = marginal(mcmc{j}, {1,2}, V, data); % reruns sampler...
    for i=1:2
      subplot2(2,2,i,1);
      [h, histArea] = plot(margApprox{i}, 'useHisto', true);
      hold on
      [h, p] = plot(margExact{i}, 'scaleFactor', histArea, ...
        'plotArgs', {'linewidth', 2, 'color', 'r'});
      title(sprintf('exact m=%5.3f, v=%5.3f', ...
        mean(margExact{i}), var(margExact{i})));
      subplot2(2,2,i,2);
      plot(margApprox{i}, 'useHisto', false);
      title(sprintf('approx m=%5.3f, v=%5.3f, Rhat=%4.3f', ...
        mean(margApprox{i}), var(margApprox{i}), convDiag.Rhat(i)));
    end
    suptitle(ttl);


    figure;
    for i=1:2
      subplot(1,2,i);
      stem(acf(S(:,i), 30));
      title(ttl)
    end
    drawnow
end

Gibbs: starting to collect 500 samples from chain 1 of 3
Gibbs: starting to collect 500 samples from chain 2 of 3
Gibbs: starting to collect 500 samples from chain 3 of 3
Gibbs: starting to collect 500 samples from chain 1 of 3
Gibbs: starting to collect 500 samples from chain 2 of 3
Gibbs: starting to collect 500 samples from chain 3 of 3
MH: starting to collect 500 samples from chain 1 of 3
MH: starting to collect 500 samples from chain 2 of 3
MH: starting to collect 500 samples from chain 3 of 3
MH: starting to collect 500 samples from chain 1 of 3
MH: starting to collect 500 samples from chain 2 of 3
MH: starting to collect 500 samples from chain 3 of 3
MH: starting to collect 500 samples from chain 1 of 3
MH: starting to collect 500 samples from chain 2 of 3
MH: starting to collect 500 samples from chain 3 of 3
MH: starting to collect 500 samples from chain 1 of 3
MH: starting to collect 500 samples from chain 2 of 3
MH: starting to collect 500 samples from chain 3 of 3

Published with MATLAB® 7.7