Matlab code for MAP estimation of DAG structures

Written by Mark Schmidt and Kevin Murphy.
Last updated 15 October 2007.

Summary

L1DAGLearn contains code for learning the structure of probabilistic Directed Acyclic Graphs (DAGs) from continuous or binary data. Linearly-parameterized conditional probability distributions are used, modeling continuous data with Gaussian distributions and binary data using Logistic Regression. It includes a DAG-Search and Order-Search strategy (where the Order-Search can use either enumeration or L1-regularization to solve the feature selection problem), and initial edge pruning can (optionally) be done using either the Sparse Candidate or the L1 Markov Blanket (L1MB) algorithm. The BIC (or AIC) score is used to measure quality during the search, and the code supports both observational and experimental (set by intervention) data.

The algorithms are described in the following paper:

Learning Graphical Model Structure using L1-Regularization Paths
M Schmidt, A Niculescu-Mizil, K Murphy.
AAAI'07
Appendix to above, with more algorithmic details and experimental results.

For code for Bayesian inference of DAGs, see BDAGL.

How to use the code

Download DAGLearn.zip
Download lars.m, taken from Karl Sjostrand's library. This is needed for the L1-based methods on continuous data (including running the demo below).

Then, in Matlab, type cd DAGLearn addpath(genpath(pwd)) example_DAGLearn

Explanation of the demo

The demo called by the above code illustrates the software's usage (the script waits for the user to press a key between running the different methods). Below, we give more detail on the commands executed in 'example_DAGLearn'.

data = 'factors'; nSamples = 10000; nEvals = 2500; discrete = 0; % Set to 1 for binary data interv = 1; % Set to 0 for observational data
The data parameter specifies the Bayes Net structure that will be used to generate the data (and that we will try to learn back in the example). The 'factors' graph is a toy 27-node structure, where the parents of each node are the nodes that factor the node number (ie. node '12' has parents '1', '2', '3', '4', and '6'). Several graph structures from the Bayesian Network Repository are also available ('alarm', 'barley', 'carpo', 'hailfinder', 'insurance', 'mildew', and 'water'). nSamples is the number of samples from the network that will be generated, and nEvals is a limit on the number of regression problems that the search algorithms will be allowed to solve. If discrete is set to 0, then continuous data will be used, setting it to 1 will use binary data. Setting interv to 0 generates purely observational data, while setting it to a value in the range [0,1] will generate samples where a randomly chosen node from each sample will be intervened on with interv probability. These parameters can be varied to test the algorithms under different scenarios (ie. set discrete to 1 to run the example on binary data, set interv to 0 to generate purely observational data, set nEvals to 10000 to allow the algorithms to search longer, set data to 'alarm' to run the example on the Alarm network, etc.). [X,clamped,DAG,nodeNames] = sampleNetwork(data,nSamples,discrete,interv);
This command samples from the selected network. X is a nSamples by (number of variables) matrix containing the samples, clamped is an indicator matrix of the same size that is set to 1 if a node was the target of an intervention (and 0 otherwise), DAG is the true generating structure, and nodeNames are the names of the individual nodes. penalty = log(nSamples)/2;
DAGLearn tries to minimize the negative log-likelihood of X, subject to penalty multiplied by the number of parameters in the model. Setting penalty to this value corresponds to the BIC score (the AIC score is obtained by setting penalty to 1). potentialParents = ones(size(X,2)); adj_DS = DAGsearch(X,nEvals,0,penalty,discrete,clamped,potentialParents,1);
These lines run an unrestricted DAG-Search algorithm (multiple restart greedy hill-climbing, using edge additions, deletions, and reversals). The parameter '0' turns off random restarting, while the last parameter turns on verbosity. Setting the indicator matrix 'potentialParents' to a matrix of ones allows any node to be a parent of any other node (subject to acyclicity). adj_OS = OrderSearch(X,nEvals,0,penalty,discrete,clamped,potentialParents);
An alternative to searching in the space of DAGs is to use a method that finds the best DAG consistent with a node ordering, and search in the space of orderings (by considering swaps in adjacent elements in the ordergin). The above uses L1-regularized (linear or logistic) regression paths to efficiently solve the feature selection problem, although the option to use enumeration (with a bound on the number of parents) is possible by changing the parameter discrete (set to 1X to search all subsets up to size X for continuous data, and -1X to search all subsets up to size X for discrete data). SC = SparseCandidate(X,clamped,10); adj_DS_SC = DAGsearch(X,nEvals,0,penalty,discrete,clamped,SC);
Allowing every node to be considered as a potential parent of every other node leads to a costly search, since we must consider a large number of operations (when searching in the space of DAGs) or solve a large feature selection problem (when searching in the space of orderings). We can significantly decrease the cost of the search by restricting the edges that we consider adding to the graph. The 'SparseCandidate' function returns a matrix of potential parents that, for each node, only includes the 10 parents with highest correlation. We then re-run DAG-Search on this substantially reduced space. [L1MB_AND,L1MB_OR] = L1MB(X,penalty,discrete,clamped,nodeNames); adj_DS_L1MB = DAGsearch(X,nEvals,0,penalty,discrete,clamped,L1MB_OR);
Looking at only pairwise statistics and using a fixed threshold on the number of parents is problematic. An alternative to using pairwise statistics is to treat the potential parent selection problem as a feature selection problem. This code uses L1-regularization paths for linear/logistic regression to select a sparse set of potential parents (the node's 'L1 Markov Blanket'). We then re-run DAG-Search yet again, with this (often better) set of potential parents. 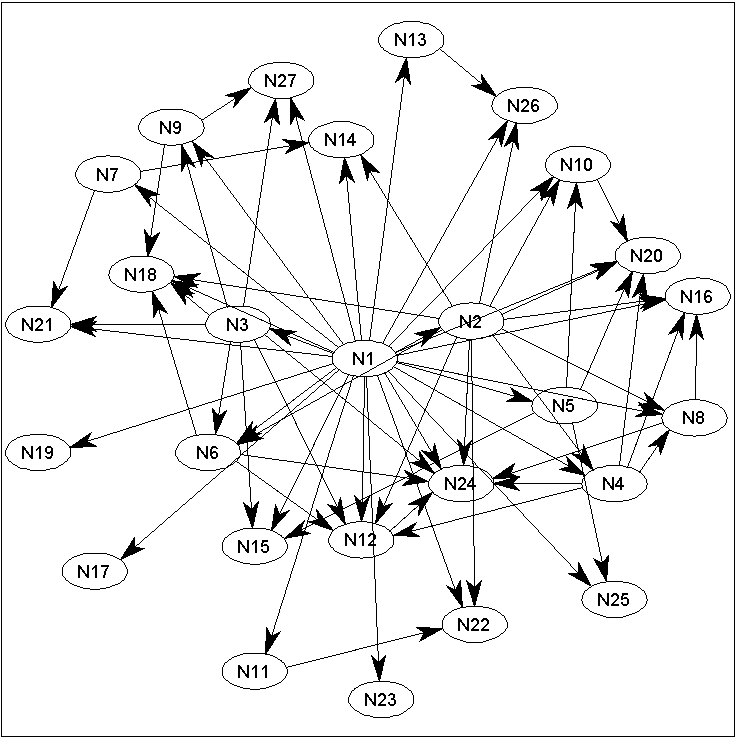err_DS = sum(adj_DS(:)~=DAG(:)) err_OS = sum(adj_OS(:)~=DAG(:)) err_DS_SC = sum(adj_DS_SC(:)~=DAG(:)) err_DS_L1MB = sum(adj_DS_L1MB(:)~=DAG(:)) drawGraph(adj_DS_L1MB,'labels',nodeNames); >> err_DS = 37 >> err_OS = 31 >> err_DS_SC = 52 >> err_DS_L1MB = 0
Finally, we output the number of structural errors made by the different methods, and draw the graph corresponding to the L1MB-pruned DAG-Search (requires Graphviz). In this case, the L1MB-pruned DAG-Search finds the true structure (in fact, the L1MB-pruned DAG-Search finds the true structure twice, while none of the other methods found it yet):