OpenBayes design
[Kevin Murphy, 30 July 2001.]
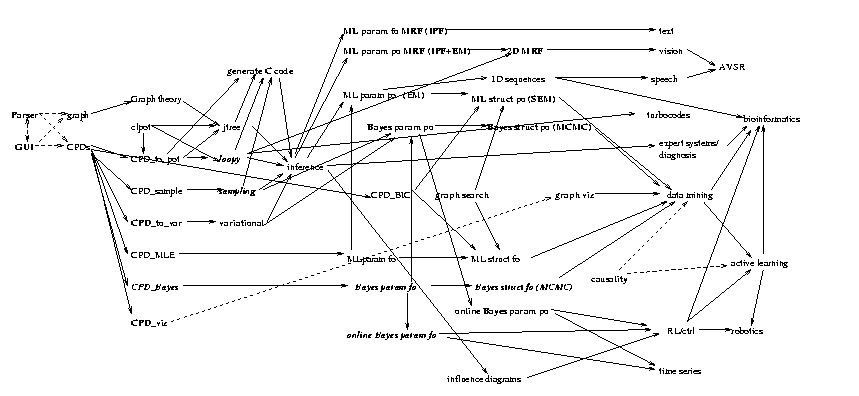
Below is a sketch of the proposed overall design of the library.
Some possible application areas are on the right hand side.
Bold means not yet implemented in BNT, italic bold means only partly
implemented in BNT, and regular (Roman) font means more or less fully
implemented in BNT.
Dotted lines means optional components.
Click on the figure for an enlargement.
The main statistical component of the project comes in defining the
CPD (Conditional Probability Distribution) classes.
These can be developed independently, and not all methods need be
implemented at once. In rough order of priority, I would include:
tabular (multinomial), conditional linear Gaussian, decision/regression
trees, generalized linear models (GLIMs - includes softmax), noisy-or,
others.
(BNT supports multinomials, Gaussians, softmax etc. It badly needs
more Bayesian inference
routines (other than just multinomials), and tree-CPDs.)
Explanation of nodes (right to left, top to bottom)
- CPD = conditional prob. distribution.
- clpot = clique potential. Comes in 4 flavors: dpot
(discrete/tabular), gpot (Gaussian), cgpot (conditional Gaussian), and
scgpot (numerically stable CG pot).
- CPD_to_pot means evaluating a CPD with any evidence, and
converting it to a potential
- MLE = max. likelihood estimate
- CPD_viz = method for visualizing the parameter values of a CPD
- graph theory = routines for computing optimal elimination
(trangulation) orderings, finding maximal cliques, etc.
- jtree = junction tree algorithm
- loopy = loopy belief propagation
- Learning can come in 8 flavors - ML/MAP point estimate or
Bayesian, parameter or
structure learning, fully observed (fo) or partially (po).
- MRF = Markov Random Field (undirected graphical model)
- IPF = iterative proportional fitting.
- EM = Expectation Maximization
- SEM = structural EM.
- MCMC = Markov Chain Monte Carlo
- BIC = Bayesian Information Criterion, used for model selection
(structure learning)
- AVSR = Audio Visual Speech Recognition
- RL/ctrl = reinforcement learning/ control theory
